Cho tam giác ABC có BN và CM là 2 đường phân giác vuông góc với nhau. Biết AB=19; AC=22. Tính độ dài BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác ABC có 2 đường phân giác BN và CM vuông góc với nhau. Biết AB=19; AC=22. Tính độ dài BC


Gọi giao điểm của BN, CM là G => G là trọng tâm của tam giác ABC
Ta có: BN vuông góc vs CM
=> BG vuông góc vs GM và CG vuông góc vs GN
=> MG2 + GB2 = BM2 =(1/2.AB)2 =90,25 và CG2 + GN2 = NC2 = (1/2AC)2 = 121 (ĐL Pytago)
=> MG2 + GB2 + CG2 + GN2 = 211,25
Mà MG = 1/2 CG và NG = 1/2 BG (Vì G là trọng tâm)
=> (1/2CG)2 + CG2 + (1/2 BG)2 + BG2 =211,25 => 5/4 BG2 + 5/4 CG2 =211,25
=> BG2 +CG2 = 211,25 : 5/4 =169
=> BC2 = 169 (Vì BG2 +CG2 = BC2) => BC = 13

Câu hỏi của Nguyễn Quang Nam - Toán lớp 8 - Học toán với OnlineMath
Tham khảo bài 3 tại link trên nhé!

a.Xét ΔDAB,ΔDMBΔ���,Δ��� có:
ˆDAB=ˆDMB(=90o)���^=���^(=90�)
Chung BD��
ˆABD=ˆMBD���^=���^
→ΔDAB=ΔDMB→Δ���=Δ���(cạnh huyền-góc nhọn)
b.Từ câu a →BA=BM,DA=DM→��=��,��=��
→B,D∈→�,�∈ trung trực AM��
→DB→�� là trung trực AM��
c.Ta có: DM⊥BC→KD⊥BC��⊥��→��⊥��
CA⊥AB→CD⊥BK��⊥��→��⊥��
→D→� là trực tâm ΔBCKΔ���
→BD⊥CK→��⊥��
→BN⊥KC→��⊥��
Xét ΔBMK,ΔBACΔ���,Δ��� có:
Chung ^B�^
BM=BA��=��
ˆBMK=ˆBAC(=90o)���^=���^(=90�)
→ΔBMK=ΔBAC(c.g.c)→Δ���=Δ���(�.�.�)
→BK=BC→��=��
→ΔKBC→Δ��� cân tại B�
d.Ta có: ΔBCKΔ��� cân tại B,BN⊥CK→N�,��⊥��→� là trung điểm KC��
Trên tia đối của tia NP�� lấy điểm F� sao cho NP=NF��=��
Xét ΔNKP,ΔNCFΔ���,Δ��� có:
NK=NC��=��
ˆKNP=ˆCNF���^=���^
NP=NF��=��
→ΔNKP=ΔNCF(c.g.c)→Δ���=Δ���(�.�.�)
→KP=CF,ˆNKP=ˆNCF→KP//CF→CF//BP→��=��,���^=���^→��//��→��//��
Xét ΔFPC,ΔBPCΔ���,Δ��� có:
ˆCPF=ˆPCB���^=���^ vì NP//BC��//��
Chung NP��
ˆPCF=ˆCPB���^=���^ vì BP//CF��//��
→ΔFPC=ΔBCP(g.c.g)→Δ���=Δ���(�.�.�)
→CF=BP→��=��
→PK=BP→��=��
→P→� là trung điểm BK��
Do E,N�,� là trung điểm BC,CK��,��
→KE,BN,CP→��,��,�� đồng quy tại trọng tâm ΔKBCΔ���

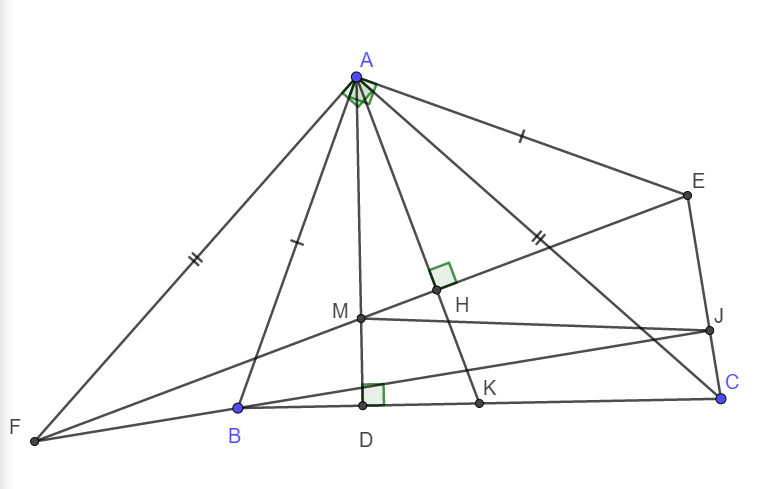
a) Xét tam giác ACK và tam giác FAM có :
AC = FA
\(\widehat{CAK}=\widehat{AFM}\) (Cùng phụ với góc \(\widehat{FAK}\) )
\(\widehat{ACK}=\widehat{FAM}\) (Cùng phụ với góc \(\widehat{DAC}\) )
\(\Rightarrow\Delta ACK=\Delta FAM\left(g-c-g\right)\)
b) Do \(\Delta ACK=\Delta FAM\left(cma\right)\Rightarrow FM=AK\)
Chứng minh hoàn toàn tương tự câu a ta có: \(\Delta ABK=\Delta EAM\left(g-c-g\right)\)
\(\Rightarrow ME=AK\)
Từ đó suy ra FM = ME hay M là trung điểm EF.
c) Kéo dài FB cắt EC tại J. Ta chứng minh \(\widehat{FJE}=90^o\)
Xét tam giác FAB và tam giác CAE có:
FA = CA
AB = AE
\(\widehat{FAB}=\widehat{CAE}\) (Cùng phụ với góc \(\widehat{BAC}\) )
\(\Rightarrow\Delta FAB=\Delta CAE\left(c-g-c\right)\)
\(\Rightarrow FB=CE\) và \(\widehat{AFB}=\widehat{ACE}\)
Xét tứ giác AFJE có:
\(\widehat{AFJ}+\widehat{FJE}+\widehat{JEA}+\widehat{EAF}=360^o\)
\(\Rightarrow\widehat{ACE}+\widehat{FJE}+\widehat{CEA}+\widehat{EAC}+90^o=360^o\)
\(\Rightarrow\widehat{FJE}+\widehat{ACE}+\widehat{CEA}+\widehat{EAC}=270^o\)
\(\Rightarrow\widehat{FJE}+180^o=270^o\)
\(\Rightarrow\widehat{FJE}=90^o\)
Vậy nên \(FB\perp EC\) (đpcm).
Bài 2:
a) Gọi giao điểm của đường phân giác ^ABC và ^ACB với AC và AB lần lượt là E và D
Dễ thấy: ^BAH=^ACB (Cùng phụ với ^HAC) => 1/2. ^BAH = 1/2. ^ACB
=> ^DAM=^ACD. Mà ^DAM+^MAC=^BAC=900 => ^ACD+^MAC=900 => AM \(\perp\)CD
hay NI\(\perp\)AM.
Tương tự ta chứng minh MI\(\perp\)AN
Xét tam giác MAN: NI\(\perp\)AM; MI\(\perp\)AN => I là trực tâm của tam giác MAN (đpcm).
b) Do I là trực tâm của tam giác AMN (cmt) => AI\(\perp\)MN hay AI\(\perp\)B'C'
Ta có: Tam giác ABC có 2 đường phân giác ^ABC và ^ACB cắt nhau tại I => AI là phân giác ^BAC
=> AI là phân giác ^B'AC'.
Xét tam giác AB'C': AI là phân giác ^B'AC'. Mà AI\(\perp\)B'C' => Tam giác AB'C' cân tại A
Lại có: ^B'AC'=900 => Tam giác B'AC' vuông cân tại A.

Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath