Cho tam giác ABC có AB = 6 cm; AC = 1 cm. Độ dài BC là số nguyên. Tam giác ABC là tam giác gì?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
22 tháng 11 2016
Áp dụng định lý Py-ta-go đảo vào tam giác ABC, có:
AB2 + AC2 = 62 + 82 = 100 = 102 = BC2
Suy ra tam giác ABC vuông
!
22 tháng 11 2016
+ Xét tam giác ABC có :
AB^2+AC^2=100
BC^2=10^2=100
=> AB^2+ AC^2= 100=BC^2
=> tam giác ABC vuông tại A ( Py-ta-go)
PT
1
24 tháng 4 2020
Ta thấy BC là cạnh lớn nhất
Ta có: \(AB^2+AC^2=6^2+8^2=100.\)
\(BC^2=10^2=100\)
\(\Rightarrow BC^2=AB^2+AC^2\)
Xét tam giác ABC có \(BC^2=AB^2+AC^2\)
=> TAM GIÁC ABC vuông tại A( Py-ta-go đảo)
23 tháng 3 2022
Hai tam giác AEF và ABF có chung đường cao hạ từ F nên ta có \(\frac{S_{AEF}}{S_{ABF}}=\frac{AE}{AB}=\frac{4}{6}=\frac{2}{3}\)(1)
Hai tam giác ABF và ABC có chung đường cao hạ từ B nên ta có \(\frac{S_{ABF}}{S_{ABC}}=\frac{AF}{AC}=\frac{4}{9}\)(2)
Từ (1) và (2) \(\Rightarrow\frac{S_{AEF}}{S_{ABF}}.\frac{S_{ABF}}{S_{ABC}}=\frac{2}{3}.\frac{4}{9}\)\(\Rightarrow\frac{S_{AEF}}{S_{ABC}}=\frac{8}{27}\)\(\Rightarrow S_{AEF}=\frac{8}{27}S_{ABC}=\frac{8}{27}.27=8\left(cm^2\right)\)
Vậy \(S_{AEF}=8cm^2\)
23 tháng 3 2022
Bạn vào thống kê hỏi đáp của mình xem câu trả lời nhé. Nó chưa duyệt lên.
3 tháng 2 2022
1: Xét ΔABC vuông tại A và ΔHBA vuông tại H có \(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
2: Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3.6\left(cm\right)\)
3: Xét ΔBAC có BK là đường phân giác
nên \(\dfrac{AK}{KC}=\dfrac{AB}{BC}\)
mà \(\dfrac{AB}{BC}=\dfrac{BH}{AB}\)
nên \(\dfrac{AK}{KC}=\dfrac{BH}{AB}\left(1\right)\)
Xét ΔAHC vuông tại H và ΔBHA vuông tại H có
\(\widehat{HAC}=\widehat{HBA}\)
Do đó: ΔAHC\(\sim\)ΔBHA
Suy ra: \(\dfrac{AC}{AB}=\dfrac{AH}{BH}\)
=>BH/AH=AB/AC
hay \(\dfrac{BH}{AB}=\dfrac{AH}{AC}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AK}{KC}=\dfrac{AH}{AC}\)
hay \(AK\cdot AC=AH\cdot KC\)
AM
28 tháng 1 2022
a. Ta có: \(AB^2+AC^2=6^2+8^2=100=BC^2\)
Áp dụng định lí Py-ta-go đảo ta có: tam giác ABC vuông tại A
b. Xét \(\Delta ABD\) vuông tại A và \(\Delta EBD\) vuông tại E có: \(\left\{{}\begin{matrix}BDchung\\\widehat{ABD}=\widehat{EBD}\end{matrix}\right.\)
\(\Rightarrow\)\(\Delta ABD\)=\(\Delta EBD\) \(\Rightarrow\)DA=DE(dpcm)
c. Xét \(\Delta FAD\) vuông tại A và \(\Delta CED\) vuông tại E có: \(\left\{{}\begin{matrix}DA=DE\\\widehat{ADF}=\widehat{EDC}\end{matrix}\right.\)
\(\Rightarrow\)\(\Delta FAD\)=\(\Delta CED\)\(\Rightarrow\)AF=EC
Mà BF=AB+BF, BC=BE+EC, AF=EC, AB=BE
\(\Rightarrow\)BF=BC\(\Rightarrow\)\(\Delta BFC\) cân tại B
d. Xét \(\Delta BFC\) cân tại B có: CA,FE là đường cao giao nhau tại D
\(\Rightarrow\)BD cũng là đường cao của \(\Delta BFC\)
mà \(\Delta BFC\) cân tại B nên BD vừa là đường cao vừa là đường trung tuyến
\(\Rightarrow\) BD là đường trung trực (dpcm)
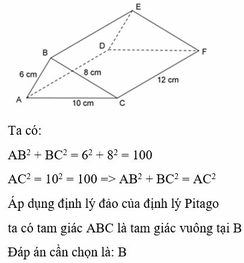
Ta có:
\(\left\{{}\begin{matrix}AB+AC=6+1=7>BC\\AB-AC=6-1=5< BC\end{matrix}\right.\Rightarrow BC=6\)(Vì BC nguyên)
Vậy ABC là tam giác cân tại B
Ta có:
{��+��=6+1=7>����−��=6−1=5<��⇒��=6{AB+AC=6+1=7>BCAB−AC=6−1=5<BC⇒BC=6(Vì BC nguyên)
Vậy ABC là tam giác cân tại B