Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a. Xét △ABM và △DCM:
\(AM=MD\left(gt\right)\)
\(\hat{AMB}=\hat{DMC}\) (đối đỉnh)
\(BM=MC\left(gt\right)\)
\(\Rightarrow\Delta ABM=\Delta DCM\left(c.g.c\right)\)
b. Từ a. => \(\hat{MCD}=\hat{MBA}\) (2 góc tương ứng). Mà hai góc này ở vị trí so le trong
\(\Rightarrow CD\text{ // }AB\left(a\right)\)
c. Xét △CIK và △AIB:
\(AI=IC\left(gt\right)\)
\(\hat{AIB}=\hat{CIK}\) (đối đỉnh)
\(BI=IK\left(gt\right)\)
\(\Rightarrow\Delta CIK=\Delta AIB\left(c.g.c\right)\Rightarrow\hat{ICK}=\hat{IAB}\). Mà hai góc ở vị trí so le trong
\(\Rightarrow AB\text{ // }CK\left(b\right)\)
Từ (a) và (b), theo tiên đề Ơ-clit \(\Rightarrow AB\text{ // }DK\)
Vậy: D, C, K thẳng hàng (đpcm).
a) Xét tam giác ABM và tam giác DCM:
BM = CM (M là trung điểm BC).
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh).
MA = MD (cmt).
\(\Rightarrow\) Tam giác ABM = Tam giác DCM (c - g - c).
b) Ta có: \(\widehat{BAM}=\widehat{CDM}\) (Tam giác ABM = Tam giác DCM).
Mà 2 góc này ở vị trí so le trong.
\(\Rightarrow\) CD // AB (dhnb).
c) Xét tứ giác AKCB có:
I là trung điểm AC (gt).
I là trung điểm BK (IB = IK).
\(\Rightarrow\) Tứ giác AKCB là hình bình hành (dhnb).
\(\Rightarrow\) CK // AB (Tính chất hình bình hành).
Mà CD // AB (cmt).
\(\Rightarrow\) D, C, K thẳng hàng.
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: BA=DC; AC=DB
Xét ΔBAC và ΔCDB có
BA=CD
AC=DB
BC chung
Do đó: ΔBAC=ΔCDB
c: Xét tứ giác AEDF có
AE//DF
AE=DF
Do đó: AEDF là hình bình hành
Suy ra: AD và FE cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của AD
nên M là trung điểm của FE
hay F,M,E thẳng hàng
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
a) Xét tam giác MAB và tam giác MDC có:
MA=MD (gt)
MB=MC( M là trung điểm BC)
\(\widehat{AMB}=\widehat{DMC}\)( đối đỉnh)
=> Tam giác MAB = tam giác MDC
b)
Tam giác MAB = tam giác MDC => \(\widehat{BAM}=\widehat{CDM}\)
Mà hai góc này ở vị trí so le trong
=> AB//CD
c) Ta có AB vuông AC
mag CD // AB
=> CD vuông AC
=> góc ACD bằng 90 độ
a: Xet ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>BD//CA
c: Xét ΔABC và ΔDCB có
AB=DC
BC chung
AC=DB
=>ΔABC=ΔDCB
d: Xét tứ giác AEDF có
AE//DF
AE=DF
=>AEDF là hình bình hành
=>AD cắt EF tại trung điểm của mỗi đường
=>E,M,F thẳng hàng
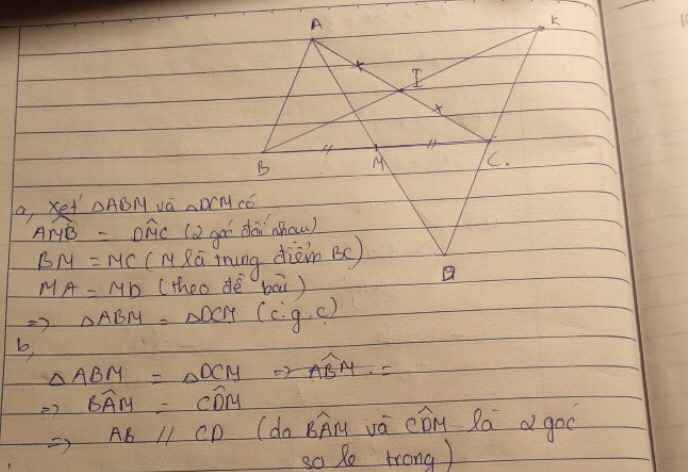
a) Xét \(\Delta MAB\)và \(\Delta MDC\)có:
MA = MD (gt)
\(\widehat{BMA}=\widehat{CMD}\)(2 góc đối đỉnh)
MB = MC (gt)
\(\Rightarrow\Delta MAB=\Delta MDC\left(c-g-c\right)\)
\(\Rightarrow AB=DC\)(2 cạnh tương ứng)
\(\widehat{BAM}=\widehat{CDM}\)(2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow AB//CD\)
b) Xét \(\Delta ACM\)và \(\Delta DBM\)có:
MA = MD (gt)
\(\widehat{AMC}=\widehat{BMD}\)(2 góc đối đỉnh)
MB = MC (gt)
\(\Rightarrow\Delta ACM=\Delta DBM\left(c-g-c\right)\)
\(\Rightarrow AC=DB\)(2 cạnh tương ứng)
Xét \(\Delta BAC\)và \(\Delta CDB\)có:
AB = DC (cmt)
AC = DB (cmt)
BC là cạnh chung
\(\Rightarrow\Delta BAC=\Delta CDB\left(c-c-c\right)\)
\(\Rightarrow\widehat{BAC}=\widehat{CDB}\)(2 góc tương ứng)
c) Bn tự lm nhá!! Phần này mk chưa nghĩ ra. Tốn chất xám lắm!!!!!