Cho tam giác ABC có B=60 ; AB=7cm: BC= 15 cm. Vẽ AH vuông góc BC (H thuộc BC ).Lấy điểm M trên HC sao HM= HB. a) So sánh BAC và ACB b) Chứng minh tam giác ABM đều. c)Tam giác ABC có phải là tam giác vuông không? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 6 2023
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
b: Xét ΔEBC có góc EBC=góc ECB
nên ΔEBC cân tại E
mà EH là đường cao
nên H là trung điểm của BC
=>HB=HC
d: Xét ΔEAI vuông tại A và ΔEHC vuông tại H có
EA=EH
góc AEI=góc HEC
=>ΔEAI=ΔEHC
=>EI=EC>EH
2 tháng 7 2023
a: góc A=90-60=30 độ
Xét ΔABC vuông tại A có sin C=AB/AC
=>6/AC=sin60
=>AC=4*căn 3(cm)
=>BC=2*căn 3(cm)
b; S ABC=1/2*2căn 3*6=6căn 3(cm2)
22 tháng 11 2021
\(a,AB=\cos B\cdot BC=6\left(cm\right)\\ AC=\sqrt{BC^2-AB^2}=6\sqrt{3}\left(cm\right)\\ b,\text{Áp dụng HTL: }AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{3}\left(cm\right)\)
25 tháng 10 2021
\(sinB=\dfrac{AC}{BC}\Rightarrow AC=sin60^0.6=3\sqrt{3}\left(cm\right)\)
\(AB=\sqrt{BC^2-AC^2}=\sqrt{6^2-\left(3\sqrt{3}\right)^2}=3\left(cm\right)\)
\(\widehat{C}=90^0-\widehat{B}=90^0-60^0=30^0\)
TP
25 tháng 10 2021
ΔABC vuông tại A có:
sinB=\(\dfrac{AC}{BC}=\dfrac{AC}{6}\)⇒AC=sin60.6=\(3\sqrt{3}cm\)
cosb=\(\dfrac{AB}{BC}=\dfrac{AB}{6}\)⇒AB=cos60.6=3cm
góc C = 90-góc B=90-30=60 độ
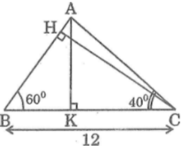
a: Xét ΔABC có AB<BC
nên \(\widehat{ACB}< \widehat{BAC}\)
b: Xét ΔAMB có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔAMB cân tại A
mà \(\widehat{B}=60^0\)
nên ΔAMB đều