Vẽ góc nhọn xOy . Trên tia Ox lấy hai điểm A và B (A nằm giữa O và B). Trên tia Oy lấy hai điểmC và D (C nằm giữa O và D) sao cho OA = OC; AB = CD.
a) Chứng minh rằng: Tam giác OAD = Tam giác OCB?
b) Chúng minh rằng: góc OAD= góc OCB; góc BAD= góc DCB?
c) Gọi I là giao điểm của AD và BC; M là trung điểm của AC. Chúng minh rằng OM là phân giác góc xOy từ đó, chúng minh O; M; I thắng hàng?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

14 tháng 2 2020
a) Xét ▲OAD và ▲OBC có :
OA = OB ( gt )
góc COD chung
OC = OD ( gt )
=> ▲OAD = ▲OBC ( c-g-c )
=> đpcm
b) Gọi giao điểm của BC và AD là M
Vì ▲OAD = ▲OBC ( c/m trên )
=> góc OCB = góc ODA ( 2 góc tương ứng )
Xét ▲ACM có góc MAC + góc ACM + góc CMA = 1800
Xét ▲BMD có góc BMD + góc MDB + góc DBM = 1800
Mà góc OCB = góc ODA ( c/m trên ) và góc CMA = góc BMD ( đối đỉnh )
=> góc CAM = góc MBD ( đpcm )

11 tháng 3 2020
Câu hỏi của nguyenvandat - Toán lớp 7 - Học toán với OnlineMath

9 tháng 12 2021
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
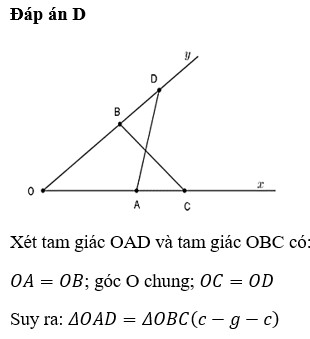


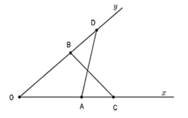


a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{DOA}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
b: Ta có: ΔOAD=ΔOCB
nên \(\widehat{OAD}=\widehat{OCB}\)
\(\Leftrightarrow\widehat{BAD}=\widehat{DCB}\)