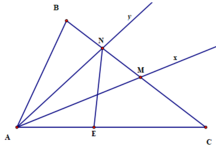
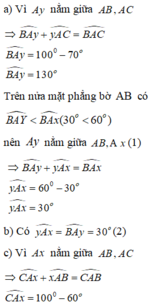1) Cho góc xAy = 90 độ. Trên cạnh Ax lấy hai điểm B và D ( D nằm giữa A và B ) , trên cạnh Ay lấy hai điểm C và E ( C nằm giữa A và E ) sao cho AD = AC ; AB = AE
a) Chứng minh : tam giác ABC = tam giác AED ; tam giác BCE = tam giác EDB
b) Đường thẳng qua A vuông góc với BC tại H và cắt DE tại M. Chứng minh M là trung điểm của DE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. cmr: BC//DE?
có: AD = 11/8 BD (GT)
=> AB = 3/8 AD
lại có: AC = 3/8 CE (GT)
mà B, D thuộc Ax (GT); C, E thuộc Ay (GT); xAy khác góc bẹt (GT)
=> BC//DE (ĐL Talet)
b. cho BC = 3cm. DE = ?
xét tam giác ADE có: BC//DE (CMT)
=> AC/AE=BC/DE=AB/AD (hệ quả ĐL Talet)
mà AC/AE=AB/AD=3/8 (GT, CMT)
=> BC/DE = 3/8
=> 8.BC=3.DE
=> 8.3=3.DE (vì BC=3 cm)
=>24=3.DE
=>DE= 8cm

a) Xét ΔABE và ΔADC có
AB=AD(gt)
\(\widehat{DAC}\) chung
AE=AC(gt)
Do đó: ΔABE=ΔADC(c-g-c)
Suy ra: BE=DC(hai cạnh tương ứng)
b) Ta có: ΔABE=ΔADC(cmt)
nên \(\widehat{ABE}=\widehat{ADC}\)(hai góc tương ứng)
mà \(\widehat{ABE}+\widehat{DBC}=180^0\)(hai góc kề bù)
và \(\widehat{ADC}+\widehat{ODE}=180^0\)(hai góc kề bù)
nên \(\widehat{OBC}=\widehat{ODE}\)
Xét ΔOBC và ΔODE có
\(\widehat{OBC}=\widehat{ODE}\)(cmt)
BC=DE
\(\widehat{OCB}=\widehat{OED}\)(ΔACD=ΔAEB)
Do đó: ΔOBC=ΔODE(g-c-g)
c) Ta có: AC=AE(gt)
nên A nằm trên đường trung trực của CE(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: MC=ME(M là trung điểm của CE)
nên M nằm trên đường trung trực của CE(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM là đường trung trực của CE(đpcm)

Tham khảo:
Kí hiệu tam giác vt là t/g nhé
a) Xét t/g AOC và t/g BOD có:
OA = OB (gt)
CAO = DBO (gt)
AC = BD (gt)
Do đó, t/g AOC = t/g BOD (c.g.c)
=> OC = OD (2 cạnh tương ứng) (1)
Tương tự ta cũng có t/g AOE = t/g BOF (c.g.c)
=> OE = OF (2 cạnh tương ứng) (2)
(1) và (2) là đpcm
b) t/g AOC = t/g BOD (câu a)
=> AOC = BOD (2 góc tương ứng)
Mà AOC + COB = 180o ( kề bù)
nên BOD + COB = 180o
=> COD = 180o
=> C,O,D thẳng hàng
trường hợp c` lại tương tự
c) Có: AC = BD (gt); AE = BF (gt)
=> AE - AC = BF - BD ( vì hình của mk AE > AC c` nếu hình bn vẽ AC > AE thì ngược lại)
=> EC = FD
Vì BAx = ABy mà 2 góc này ở vị trí so le trong nên Ax // By
Xét t/g CEO và t/g DFO có:
CEO = DFO (so le trong)
EC = FD (cmt)
ECO = FDO (so le trong)
Do đó, t/g CEO = t/g DFO (g.c.g)
=> CO = DO (2 cạnh tương ứng)
EO = FO (2 cạnh tương ứng)
Từ đó dễ dàng suy ra t/g COF = t/g DOE (c.g.c)
=> CF = DE (2 cạnh tương ứng) (đpcm)

Tham khảo
Kí hiệu tam giác vt là t/g nhé
a) Xét t/g AOC và t/g BOD có:
OA = OB (gt)
CAO = DBO (gt)
AC = BD (gt)
Do đó, t/g AOC = t/g BOD (c.g.c)
=> OC = OD (2 cạnh tương ứng) (1)
Tương tự ta cũng có t/g AOE = t/g BOF (c.g.c)
=> OE = OF (2 cạnh tương ứng) (2)
(1) và (2) là đpcm
b) t/g AOC = t/g BOD (câu a)
=> AOC = BOD (2 góc tương ứng)
Mà AOC + COB = 180o ( kề bù)
nên BOD + COB = 180o
=> COD = 180o
=> C,O,D thẳng hàng
trường hợp c` lại tương tự
c) Có: AC = BD (gt); AE = BF (gt)
=> AE - AC = BF - BD ( vì hình của mk AE > AC c` nếu hình bn vẽ AC > AE thì ngược lại)
=> EC = FD
Vì BAx = ABy mà 2 góc này ở vị trí so le trong nên Ax // By
Xét t/g CEO và t/g DFO có:
CEO = DFO (so le trong)
EC = FD (cmt)
ECO = FDO (so le trong)
Do đó, t/g CEO = t/g DFO (g.c.g)
=> CO = DO (2 cạnh tương ứng)
EO = FO (2 cạnh tương ứng)
Từ đó dễ dàng suy ra t/g COF = t/g DOE (c.g.c)
=> CF = DE (2 cạnh tương ứng) (đpcm)
a: Xét tứ giác ACBD có
AC//BD
AC=BD
Do đó: ACBD là hình bình hành
Suy ra: Hai đường chéo AB và CD cắt nhau tại trung điểm của mỗi đường
mà O là trung điểm của AB
nên O là trung điểm của CD
=>C,O,D thẳng hàng
b: Xét tứ giác AEBF có
AE//BF
AE=BF
Do đó: AEBF là hình bình hành
Suy ra: Hai đường chéo AB và FE cắt nhau tại trung điểm của mỗi đường
mà O là trung điểm của AB
nên O là trung điểm của FE
hay F,O,E thẳng hàng