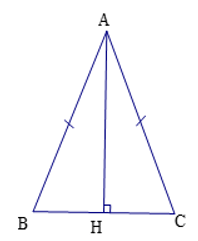
Cho tam giác ABC cân tại A, AB > BC, H là trung điểm của BC.
a) Chứng minh: tam giác AHB = tam giác AHC. Từ đó suy ra AH vuông góc với BC.
b) Tính độ dài AH nếu BC = 4cm; AB = 6cm.
c) Tia phân giác của góc B cắt AH tại I. Chứng minh tam giác BIC cân.
d) Đường thẳng đi qua A và song song với BC cắt tia BI, CI lần lượt tại M, N. Chứng minh rằng: A là trung điểm của MN.
e) Kẻ IE vuông góc với AB, IF vuông góc với AC. Chứng minh IE = IF = IH.
f) Chứng minh IC vuông góc với MC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
Do đó: ΔAHB=ΔAHC
Ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là đường cao
b: Xét tứ giác ABIC có
H là trung điểm của BC
H là trung điểm của AI
Do đó: ABIC là hình bình hành
Suy ra: IB=AC

a) Xét \(\Delta\)AHB và \(\Delta\)AHC có:
AB=AC (\(\Delta\)ABC cân tại A)
BH=HC (H là trung điểm BC)
AH chung
=> △AHB=△AHC (c.c.c)
b) Xét △ABC có H là trung điểm BC
=> AH là đường trung tuyến của △ABC
mà △ABC cân tại A (gt) => AH trùng với đường cao
=> AH _|_ BC. Mà H là trung điểm BC
=> AH là đường trung trực của BC (đpcm)
b) Có H là trung điểm BC => \(BH=CH=\frac{BC}{2}\)mà BC=10cm
=> \(BH=CH=\frac{10}{2}=5cm\)
Có AH _|_ BC (cmt) => △ABH cân tại H
Áp dụng định lý Pytago vào △ABH vuông tại H, ta có:
AH2+BH2=AB2
=> AH2=AB2-BH2
Thay BH=5(cm); AB=13(cm)
=> AH2=132-52
=> AH2=144
=> AH=12(cm) (AH>0)

a) Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: HB=HC(H là trung điểm của BC)
nên H nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AH là đường trung trực của BC
hay AH⊥BC(Đpcm)
b) Ta có: H là trung điểm của BC(gt)
nên \(BH=\dfrac{BC}{2}=\dfrac{30}{2}=15\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABH vuông tại H,ta được:
\(AB^2=BH^2+AH^2\)
\(\Leftrightarrow AH^2=AB^2-BH^2=25^2-15^2=400\)
hay AH=20(cm)
Vậy: AH=20cm

Giải
b)Xét tam giác BAH và CAH có:
AB=AC(gt)
góc B =góc C(gt)
AH chung
\(\Rightarrow\)tam giác BAH =CAH (c.g.c)
\(\Rightarrow\)góc BAH=CAH (2 góc t/ư)
Mặt khác AH nằm giữa AB và AC ,chia góc A thành 2 góc bằng nhau
Mà H là trung điểm BC
\(\Rightarrow\)AH là tia phân giác góc A và vuông góc BC

đề có sai không zợ
nói tg ABC cân mà AB>AC
a)\(\text{ Xét }\Delta ABH\)\(\text{và }\Delta ACH\)\(\text{có}\)
\(AB=AC\)
\(\widehat{ABH}=\widehat{ACH}\left(\Delta\text{ABC cân}\right)\)
\(BH=CH\)
\(\Rightarrow\Delta ABH=\Delta ACH\left(c.g.c\right)\)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}\)
\(\text{Mà }\widehat{AHB}+\widehat{AHC}=180^o\)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}=90^o\)
\(\Rightarrow AH\perp BC\)
b) \(\text{Có }BH=\frac{BC}{2}\left(gt\right)\)
\(\text{Mà BC = 4 ( GT )}\)
\(\Rightarrow BH=4cm\)
\(\text{Áp dụng định lý Py-ta-go vào tam giác ABH vuông tại H ta được :}\)
\(\text{AH^2 + BH^2 = AB^2}\)
\(\Rightarrow AH^2+2^2=6^2\)
\(\text{=> AH^2 = 32}\Rightarrow AH^2=32\)\(\Rightarrow AH^2=32\)
\(\Rightarrow AH=\sqrt{32}\)
\(\text{Vậy }AH=\sqrt{32}\)

a) Xét hai tam giác AMH và NMB có:
MA = MN (gt)
MB = MH (M là trung điểm BH)
ˆAMH=ˆBMNAMH^=BMN^ (đối đỉnh)
⇒ΔAMH=ΔNMB(c.g.c)⇒ΔAMH=ΔNMB(c.g.c)
Vì ΔAMH=ΔNMB(c.g.c)ΔAMH=ΔNMB(c.g.c) nên góc H = góc B
Mà ˆH=900H^=900 nên ˆB=ˆH=900B^=H^=900 (yttu)
Do đó BC⊥NBBC⊥NB
b) Ta có AH = NB (do ΔAMH=ΔNMB(c.g.c)ΔAMH=ΔNMB(c.g.c))
Vì AH là đường cao của tam giác cân ABC nên AH < AB
Do đó NB < AB
c) Ta có ˆMAH=ˆMNBMAH^=MNB^ (do ΔAMH=ΔNMB(c.g.c)ΔAMH=ΔNMB(c.g.c))
Vì NB < AB nên góc BAM < góc MNB (quan hệ góc và cạnh đối diện trong tam giác ABN)
Do đó góc BAM < góc MAH
d) Vì tam giác ABC cân tại A có AH vuông BC nên AH đồng thời là đường trung trực BC
Mặt khác, I nằm trên đường trung trực BC nên A, H, I thẳng hàng
a) Xét ΔAMH và ΔNMB có
MA=MN(gt)
\(\widehat{AMH}=\widehat{NMB}\)(hai góc đối đỉnh)
MH=MB(M là trung điểm của BH)
Do đó: ΔAMH=ΔNMB(c-g-c)
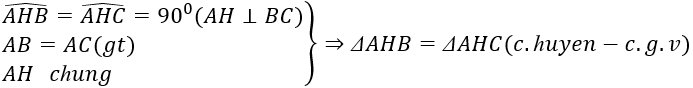
Trả lời:
P/s: Xin lỗi nha!~Chỉ đc mỗi câu a!!!~
a) Theo giả thiết ta có :
AH là đường trung tuyến ⇒BH=HC⇒BH=HC
xét ΔAHBΔAHB và ΔAHCΔAHC có:
AB=ACAB=AC (gt)
AHAH chung
BH=HCBH=HC ( cmt)
⇒ΔAHB=ΔAHC⇒ΔAHB=ΔAHC (c.c.c)
⇒AHBˆ=AHCˆ⇒AHB^=AHC^ (2 góc tương ứng )
~Học tốt!~
b , Ta có : HB +HC= Bc
mà : HB=HC (GT)
=> HB=HC=\(\frac{BC}{2}\)=\(\frac{4}{2}\)= 2
Ta có : \(\Delta ABH\)vuông tại H
=> \(AB^2\)= \(BH^2\)+ \(AH^2\)( Định lí Py-ta-go)
=> 62 = 22 + AH2
=> AH2 = 62 - 22
=> AH2 = 32
=> AH \(\approx\) 5,7 cm