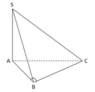
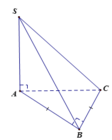
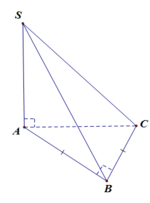
Cho hình chóp S.ABC có SA vuông góc với A B C , A B = a ; A C = a 2 , B A C ⏜ = 45 ° . Gọi B 1 , C 1 lần lượt là hình chiếu vuông góc của A lên S B , S C . Tính thể tích mặt cầu ngoại tiếp hình chóp A . B C C 1 B 1 .
A. V = π a 3 2 3
B. V = π a 3 2
C. V = 4 3 π a 3
D. V = π a 3 2

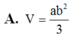
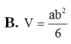
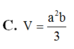
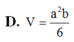
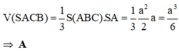
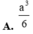
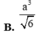
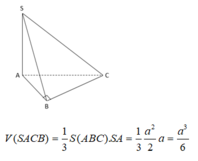
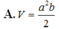
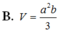
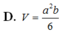
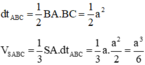

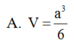
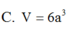
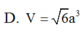
Đáp án A
Dễ thấy Δ A B C là tam giác vuông cân tại B, do đó O A = O B = O C (với O là trung điểm của AC)
Ta có B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ A B 1 , lại do A B 1 ⊥ S B ⇒ A B 1 ⊥ B 1 C
Do đó Δ A B 1 C vuông tại O nên O A = O C = O B 1
Vậy O là tâm mặt cầu ngoại tiếp hình chóp A B C C 1 B 1
Do đó R = A C 2 = a 2 2 ⇒ V = 4 3 π R 3 = π a 3 2 3