Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Đồ thị hàm số y = ax + b đi qua A(1; 3) và B(-1; -1)
Vậy a = 2; b = 1; hàm số y = 2x + 1.
b) y = ax + b song song với y = x + 5
⇒ a = 1.
Đồ thị hàm số đi qua C(1; 2) ⇔ 2 = a.1 + b ⇔ a + b = 2 ⇒ b = 1.
Vậy a = 1; b = 1.
a) Đồ thị hàm số y = ax + b đi qua A(1; 3) và B(-1; -1)
Vậy a = 2; b = 1; hàm số y = 2x + 1.
b) y = ax + b song song với y = x + 5
⇒ a = 1.
Đồ thị hàm số đi qua C(1; 2) ⇔ 2 = a.1 + b ⇔ a + b = 2 ⇒ b = 1.
Vậy a = 1; b = 1.
a. \(PTHDGD:\left(d\right)-\left(d'\right):2x+3=x-1\)
\(\Rightarrow x=-4\left(1\right)\)
Thay (1) vào (d'): \(y=-4-1=-5\)
\(\Rightarrow M\left(-4;-5\right)\)
\(a,\text{PT hoành độ giao điểm: }2x+3=x-1\\ \Leftrightarrow x=-4\Leftrightarrow y=-5\\ \Leftrightarrow M\left(-4;-5\right)\\ b,\Leftrightarrow\left\{{}\begin{matrix}-2a+b=3\\a=2;b\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=7\end{matrix}\right.\)
vì dths y=ax+b // với dt (d) => a=2
mà đths y=ax+b đi qua điểm B =>2=2.(-1)+b =>b=4
vì dths y=ax+b // với dt (d) => a=2
mà đths y=ax+b đi qua điểm B =>2=2.(-1)+b =>b=4
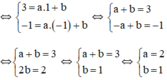
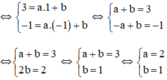
Ta có: 2x+y=3 \(\Leftrightarrow\) y=-2x-3
a) Vì hs y=ax+b song song với đt y=-2x-3 nên\(\hept{\begin{cases}a=-2\\b\ne-3\end{cases}}\)
Suy ra pt y = ax + b là y = -2x + b (b\(\ne\)-3)
Mặt khác đt này lại đi qua điểm M(2;5) nên khi x=2 thì y=5. Ta có phương trình:
-2.2+b=5 \(\Leftrightarrow\)-4+b=5 \(\Leftrightarrow\) b=9
Vậy.......