Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
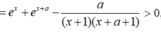
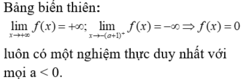
Đáp án C.
Ta có
log b a 2018 = log b a 2018 ⇔ log b a 2018 = 2018 log b a ⇔ log b a = 0 log b a 2017 = 2018
⇔ a = 1 log b a = 2018 2017 ⇔ a = 1 a = b 2018 2017
Do a là số thực dương nên với mỗi số nguyên b thỏa mãn điều kiện 2 ≤ b ≤ 200 thì sẽ tạo ra một cặp số a ; b thỏa mãn yêu cầu đề bài.
Do vậy có 2 × 200 − 2 1 + 1 = 398 cặp. Vậy ta chọn C.
Lời giải sai: log b a 2018 = 2018 log b a ⇔ log b a 2017 = 2018 , tức là bỏ mất trường hợp log b a = 0 , từ đó dẫn đến chọn đáp án B
từ 100 đến 200 có (200-100):1+1 = 101 số -dãy trên bắt đầu là số chẵn và kết thúc là số chẵn nên số số chẵn hơn số số lẻ là 1 số. vậy có 50 số chẵn và 51 số lẻ. - Từ 101 -> 109 có 9 chữ số 0. - Từ 110 - 190 có 9 chữ số 0 - số 100 và 200 có 4 chữ số 0 vậy tổng cộng có 9 x2 + 4 = 22 chữ số 0
Từ 100 đến 200 có (200-100):1+1 = 101 số
-dãy trên bắt đầu là số chẵn và kết thúc là số chẵn nên số số chẵn hơn số số lẻ là 1 số.
vậy có 50 số chẵn và 51 số lẻ.
- Từ 101 -> 109 có 9 chữ số 0.
- Từ 110 - 190 có 9 chữ số 0
- số 100 và 200 có 4 chữ số 0
Vậy tổng cộng có 9 x2 + 4 = 22 chữ số 0
Ta có : \(3675=3.5^2.7^2\)
Số 3675 có 18 ước
\(200=2^3.5^2\)
Số 200 có 12 ước
\(119=7.17\)
Số 119 có 4 ước
