Trên mặt phẳng Oxy, cho hai điểm A(1; 3), B(4; 2).
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB;
b) Tính chu vi tam giác OAB.
c) Chứng tỏ OA vuông góc với AB và từ đó tính diện tích tam giác OAB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường thẳng đi qua hai điểm A và B có dạng: y = ax + b
Đường thẳng đi qua hai điểm A và B nên tọa độ A và B nghiệm đúng phương trình.
Ta có: Tại A: 2 = a + b ⇔ b = 2 – a (1)
Tại B: 4 = 3a + b (2)
Thay (1) và (2) ta có: 4 = 3a + 2 – a ⇔ 2a = 2 ⇔ a = 1
Vậy hệ số a của đường thẳng đi qua A và B là 1.

Đáp án C
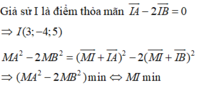
Suy ra M là hình chiếu vuông góc của I lên (Oxy) => I(3;-4;0)

Đáp án A.
Cách giải:
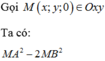
![]()
Thử lần lượt 4 đáp án thì ta thấy với M(3;-4;0)
thì M A 2 - 2 M B 2 = 3 là lớn nhất.

I nằm trên d nên I(x;-2x-5)
IA=IB=R
=>(x-1)^2+(-2x-5+3)^2=(x+3)^2+(-2x-5-1)^2
=>x^2-2x+1+4x^2+8x+4=x^2+6x+9+4x^2+24x+36
=>6x+5=30x+45
=>-24x=40
=>x=-5/3
=>I(-5/3;-5/3)
A(1;-3)
=>R=4/3*căn 5
=>(C): (x+5/3)^2+(y+5/3)^2=80/9

Đường thẳng đi qua hai điểm A và B có dạng: y = ax + b
Thay a = 1 vào (1) ta có: b = 2 – 1 = 1
Vậy phương trình đường thẳng AB là y = x + 1

Đáp án A
- A: B có hoành độ là hoành độ của 2 đỉnh của 2 bán trục lớn của (E) , chúng nằm trên đường thẳng y+ 2= 0. Điểm C có hoành độ và tung độ dương thì C nằm trên cung phần tư thứ nhất
- Tam giác ABC có AB= 6 cố định. Vì thế tam giác có diện tích lớn nhất khi khoảng cách từ C đến AB lớn nhất.
- Dễ nhận thấy C trùng với đỉnh của bán trục lớn (0; 3).
a) D nằm trên trục Ox nên D có tọa độ D(x ; 0)
Khi đó :
Vậy chu vi tam giác OAB là P = AO + BO + AB = √10 + 2√5 + √10 = 2√5 + 2√10