Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xét phương án C:
(C) tiếp xúc với trục Oy khi d ( I ; y ' O y ) = R ⇔ a = R .
Do đó đáp án (C) sai vì nếu a= -9 => R= -9 < 0 (vô lý)
Chọn C.
Ta có: đường tròn (C1) :
Vậy (1) đúng
Đường tròn ( C2):
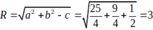
Vậy (2) đúng.
Chọn C.
+Ta có a= -4; b= -3 ; c= 9 và a2+ b2- c= 16+ 9 - 9 = 16> 0
Suy ra (C) là đường tròn tâm I( -4; -3) và R= 4
Vậy B; C đúng.
+Thay O vào (C) ta có: 02+ 02+ 8.0+ 6.0 + 9= 0 vô lí . Vậy A đúng.
+Thay M( -1; 0) vào (C) ta có: (-1) 2+ 02+ 8.(-1) + 6.0 + 9= 0 ( vô lý). Vậy D sai.
Chọn D.
Ta có: a= 2; b= -m và c= m2; a2+b2- c= 4> 0 nên A; D đúng.
Vì a= R = 2 nên B đúng.
Từ đó suy ra C sai, vì đường tròn tiếp xúc với x’Ox khi và chỉ khi |b|=|m|=2 ⇔ m = ± 2
Chọn C.
Đường tròn (C): x 2 + y 2 + 4 x − 6 y − 3 = 0 có tâm I(-2; 3) và bán kính R = 4.
Khoảng cách d I , ∆ = 3. − 2 − 4.3 − 2 5 = 4 nên đường thẳng tiếp xúc đường tròn.
ĐÁP ÁN B
Cách 1 : Xác định các hệ số a, b, c.
a) x2 + y2 – 2x – 2y – 2 = 0 có hệ số a = 1 ; b = 1 ; c = –2
⇒ tâm I (1; 1) và bán kính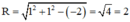 
b) 16x2 + 16y2 + 16x – 8y –11 = 0
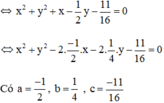
⇒ Đường tròn có tâm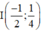 
, bán kính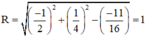 
c) x2 + y2 - 4x + 6y - 3 = 0
⇔ x2 + y2 - 2.2x - 2.(-3).y - 3 = 0
có hệ số a = 2, b = -3,c = -3
⇒ Đường tròn có tâm I(2 ; –3), bán kính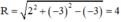 
Cách 2 : Đưa về phương trình chính tắc :
a) x2 + y2 - 2x - 2y - 2 = 0
⇔ (x2 - 2x + 1) + (y2 - 2y +1) = 4
⇔(x-1)2 + (y-1)2 = 4
Vậy đường tròn có tâm I(1 ; 1) và bán kính R = 2.
b) 16x2 + 16y2 + 16x - 8y - 11 = 0
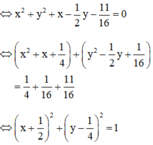
Vậy đường tròn có tâm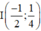 
và bán kính R = 1.
c) x2 + y2 - 4x + 6y -3 = 0
⇔ (x2 - 4x + 4) + (y2 + 6y + 9) = 4 + 9 + 3
⇔ (x - 2)2 + (y + 3)2 = 16
Vậy đường tròn có tâm I( 2 ; –3) và bán kính R = 4.
Ta xét các phương án:
(I) có:
(II) có:
(III) tương đương : x2+ y2 – 2x - 3y + 0,5= 0.
phương trình này có:
Vậy chỉ (I) và (III) là phương trình đường tròn.
Chọn D.
Đáp án: D
Ta có:
(C): x 2 + y 2 + 4x + 6y + 3 = 0 ⇔ (x + 2 ) 2 + (y + 3 ) 2 = 10
Vậy I(-2;-3), R = 10
Cho x= 0 ta được: y2+ 3= 0 phương trình vô nghiệm.
Vậy (C) không có điểm chung nào với trục tung.
Chọn D.