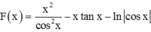Cho y = x cos 2 x trên - π 2 ; π 2 và F(x) là một nguyên hàm của hàm số xf ‘(x) thỏa mãn F(0) = 0. Biết a ∈ - π 2 ; π 2 thỏa mãn tan a = 3. Tính F(a) – 10a2 + 3a
A. 1 2 ln 10
B. - 1 4 ln 10
C. - 1 2 ln 10
D. ln 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(sin\left(x-\dfrac{\pi}{2}\right)+cos\left(x-\pi\right)+tan\left(\dfrac{5\pi}{2}-x\right)+tan\left(x-\dfrac{\pi}{2}\right)\)
\(=-sin\left(\dfrac{\pi}{2}-x\right)+cos\left(\pi-x\right)+tan\left(2\pi+\dfrac{\pi}{2}-x\right)-tan\left(\dfrac{\pi}{2}-x\right)\)
\(=-cosx-cosx+tan\left(\dfrac{\pi}{2}-x\right)-cotx\)
\(=-2cosx+cotx-cotx=-2cosx\)

pi<x<3/2pi
=>cosx<0
pi<x<3/2pi
=>pi/2<1/2x<3/4pi
=>cos(x/2)<0
1+tan^2x=1/cos^2x
=>1/cos^2x=1+8=9
=>cosx=-1/3
\(cosx=2\cdot cos^2\left(\dfrac{x}{2}\right)-1\)
=>\(2\cdot cos^2\left(\dfrac{x}{2}\right)=\dfrac{2}{3}\)
=>\(cos^2\left(\dfrac{x}{2}\right)=\dfrac{1}{3}\)
=>cos(x/2)=1/căn 3

a) √2 cos(x - π/4)
= √2.(cosx.cos π/4 + sinx.sin π/4)
= √2.(√2/2.cosx + √2/2.sinx)
= √2.√2/2.cosx + √2.√2/2.sinx
= cosx + sinx (đpcm)
b) √2.sin(x - π/4)
= √2.(sinx.cos π/4 - sin π/4.cosx )
= √2.(√2/2.sinx - √2/2.cosx )
= √2.√2/2.sinx - √2.√2/2.cosx
= sinx – cosx (đpcm).

\(A=\frac{1}{2}+\frac{1}{2}cos2x+\frac{1}{2}+\frac{1}{2}cos\left(2x+\frac{4\pi}{3}\right)+\frac{1}{2}+\frac{1}{2}cos\left(2x-\frac{4\pi}{3}\right)\)
\(=\frac{3}{2}+\frac{1}{2}cos2x+cos2x.cos\frac{4\pi}{3}\)
\(=\frac{3}{2}+\frac{1}{2}cos2x-\frac{1}{2}cos2x=\frac{3}{2}\)
\(B=\frac{1}{2}-\frac{1}{2}cos2x+\frac{1}{2}-\frac{1}{2}cos\left(2x+\frac{4\pi}{3}\right)+\frac{1}{2}-\frac{1}{2}cos\left(2x-\frac{4\pi}{3}\right)\)
\(=\frac{3}{2}-\frac{1}{2}cos2x-cos2x.cos\frac{4\pi}{3}\)
\(=\frac{3}{2}-\frac{1}{2}cos2x+\frac{1}{2}cos2x=\frac{3}{2}\)
Đáp án A
Phương pháp: Sử dụng phương pháp tích phân từng phần tính F(x)
Cách giải:
=>