Bài 1: Cho ∆MNP vuông tại M; đường cao MI. Biết và MI = 9,8cm a/ Tính MN; MP; NP b/ Tính diện tích tam giác MIP Bài 2: Cho ∆CDE có 3 góc nhọn, đường cao CH. Gọi M, N theo thứ tự là hình chiếu của H trên CD; CE. a/ Chứng minh : CD. CM = CE. CN b/ Chứng minh ∆CMN đồng dạng với ∆CED.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


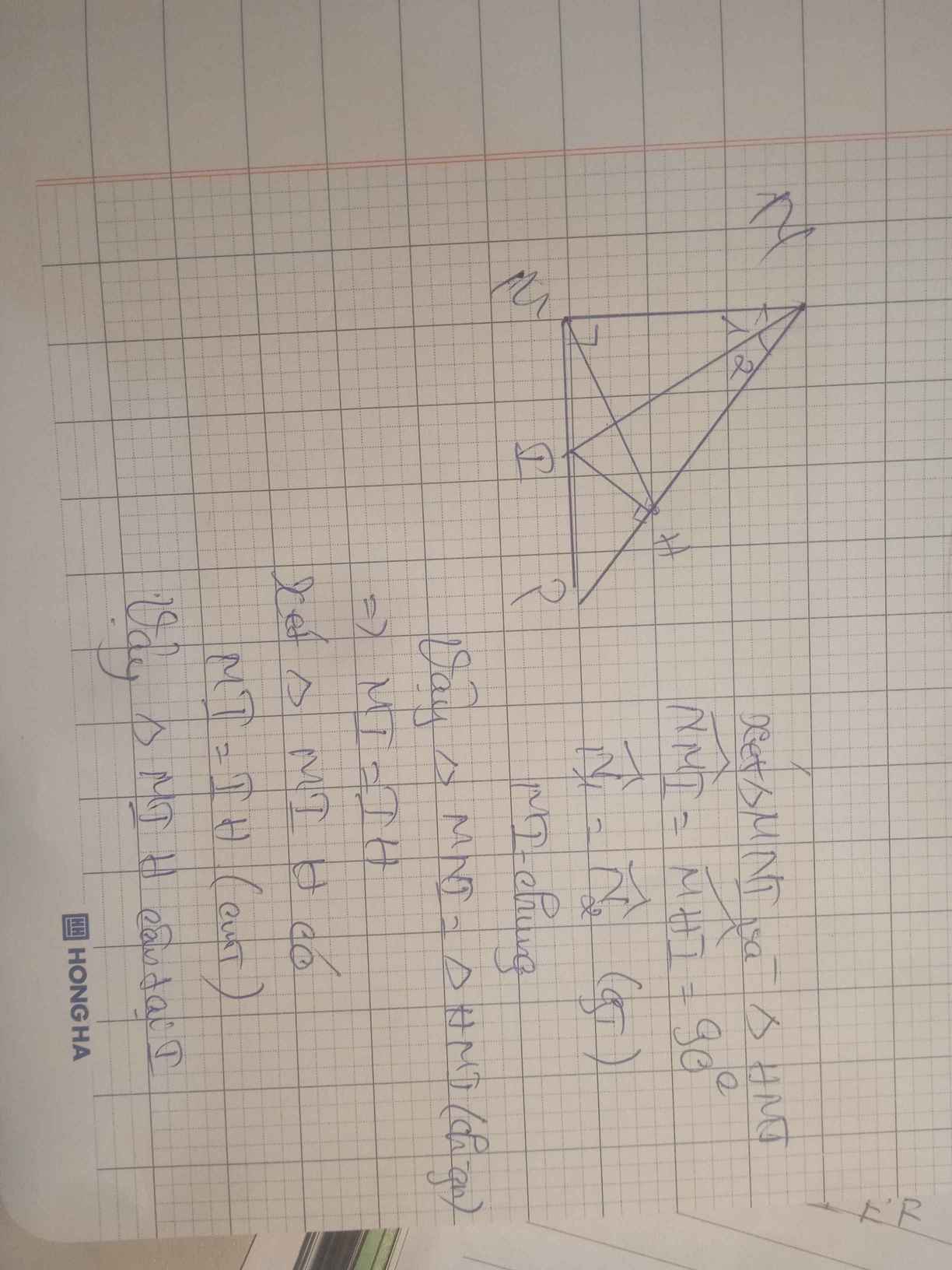
Bài 2:
\(\cos\widehat{A}=\dfrac{3\sqrt{39}}{20}\)
\(\tan\widehat{A}=\dfrac{7}{20}:\dfrac{3\sqrt{39}}{20}=\dfrac{7}{3\sqrt{39}}=\dfrac{7\sqrt{39}}{117}\)
\(\cot\widehat{A}=\dfrac{3\sqrt{39}}{7}\)

Áp dụng định lí Pytago vào ΔMNP vuông tại M, ta được:
\(MN^2+MP^2=NP^2\)
\(\Leftrightarrow MP^2=3^2-\left(\sqrt{5}\right)^2=4\)
hay MP=2cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔMNP vuông tại M có MK là đường cao ứng với cạnh huyền NP, ta được:
\(\left\{{}\begin{matrix}MN^2=NK\cdot NP\\MK\cdot NP=MN\cdot MP\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}KN=\dfrac{5}{9}\left(cm\right)\\MK=\dfrac{2\sqrt{5}}{3}\left(cm\right)\end{matrix}\right.\)
Xét ΔNMK vuông tại K có
\(\sin\widehat{NMK}=\dfrac{KN}{MN}=\dfrac{\sqrt{5}}{9}\)
\(\cos\widehat{NMK}=\dfrac{MK}{MN}=\dfrac{2}{3}\)
\(\tan\widehat{NMK}=\dfrac{KN}{KM}=\dfrac{\sqrt{5}}{6}\)
\(\cot\widehat{NMK}=\dfrac{KM}{KN}=\dfrac{6\sqrt{5}}{5}\)

Bài 1 :
Xét tam giác MNP vuông tại M, đường cao MH
* Áp dụng hệ thức : \(MH^2=NH.HP\Rightarrow NH=\frac{MH^2}{HP}=\frac{36}{9}=4\)cm
=> NP = HN + HP = 4 + 9 = 13 cm
* Áp dụng hệ thức : \(MN^2=NH.NP=4.13\Rightarrow MN=2\sqrt{13}\)cm
* Áp dụng hệ thức : \(MP^2=PH.NP=9.13\Rightarrow MP=3\sqrt{13}\)cm
Bài 2 :
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AB^2}\Rightarrow\frac{1}{9}=\frac{1}{25}+\frac{1}{AB^2}\Rightarrow AB=\frac{15}{4}\)cm
( bạn nhập biểu thức trên vào máy tính cầm tay rồi shift solve nhé )
* Áp dụng hệ thức : \(AC.AB=AH.BC\Rightarrow BC=\frac{\frac{15}{4}.5}{3}=\frac{25}{4}\)cm