Giải các hệ phương trình sau bằng phương pháp thế:
a) \(\left\{{}\begin{matrix}x\sqrt{2}-y\sqrt{3}=1\\x+y\sqrt{3}=\sqrt{2}\end{matrix}\right.; \)
b) \(\left\{{}\begin{matrix}x-2\sqrt{2}y=\sqrt{5}\\x\sqrt{2}+y=1-\sqrt{10}\end{matrix}\right.; \)
c) \(\left\{{}\begin{matrix}(\sqrt{2}-1)x-y=\sqrt{2}\\x+(\sqrt{2}+1)y=1\end{matrix}\right.. \)

a)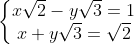
Từ phương trình (2) ⇔ x = √2 - y√3 (3)
Thế (3) vào (1): ( √2 - y√3)√2 - y√3 = 1
⇔ √3y(√2 + 1) = 1 ⇔ y =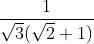 =
= 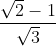
Từ đó x = √2 -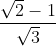 . √3 = 1.
. √3 = 1.
Vậy có nghiệm (x; y) = (1;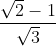 )
)
b)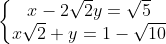
Từ phương trình (2) ⇔ y = 1 - √10 - x√2 (3)
Thế (3) vào (1): x - 2√2(1 - √10 - x√2) = √5
⇔ 5x = 2√2 - 3√5 ⇔ x =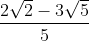
Từ đó y = 1 - √10 -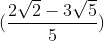 . √2 =
. √2 = 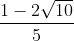
Vậy hệ có nghiệm (x; y) =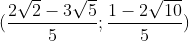 ;
;
c)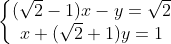
Từ phương trình (2) ⇔ x = 1 - (√2 + 1)y (3)
Thế (3) vào (1): (√2 - 1)[1 - (√2 + 1)y] - y = √2 ⇔ -2y = 1 ⇔ y = -
Từ đó x = 1 - (√2 + 1)(- ) =
) = 
Vậy hệ có nghiệm (x; y) = ( ; -
; - )
)