Cho: a,b∈ Z; (a,b)=1. CMR: \(\frac{8a+3b}{5a+2b}\) Tối giản
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b/ \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}\)
\(\Rightarrow\left(\dfrac{a}{b}\right)^3=\dfrac{a}{d}\left(1\right)\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{a+b+c}{b+c+d}\)
=> \(\left(\dfrac{a}{b}\right)^3=\left(\dfrac{a+b+c}{c+d+b}\right)^3\) (2)Từ (1) và (2)=>đpcm

Bài 1: áp dụng tính chất dãy tỉ số bằng nhau ta được:
(a+b-c)/c=(b+c-a)/a=(c+a-b)/b=(a+b-c+b+c-a+c+a-b)/(a+b+c)=(a+b+c)/(a+b+c0=1
Do đó: (a+b+c)/c=1 suy ra a+b+c=c suy ra a+b=c-c=0 nên a=b (1)
(b+c-a)/a=1 suy ra b+c-a=a suy ra a+c-a=a (b=a) suy ra c=a (2) Từ (1) và(2) ta có: a=b=c
Suy ra:P= (1+b/a).(1+c/b).(1+a/c)=(1+a/a).(1+a/a).(1+a/a)=(1+1).(1+1).(1+1)=2.2.2=8
Bài 2: bạn cũng áp dụng tính chất dãy tỉ bằng nhau rồi xét giống bài 1 là ra




Cho a thuộc Z+,b thuộc Z- .Hãy so sánh IaI,IbI trong các trường hợp sau:
a)a+b thuộc Z+
b)a+b thuộc Z-


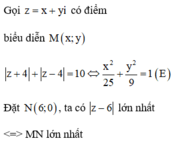
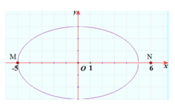
Vẽ trên hệ trục Oxy, nhận thấy MN lớn nhất khi M. Khi đó ![]()
Chọn B
\(\frac{8a+3b}{5a+2b}=\frac{5a+3a+b+2b}{5a+2b}=\frac{5a+2b}{5a+2b}+\frac{3a+b}{5a+2b}=1+\frac{3a+b}{5a+2b}\)
3a+b và 5a+2b là nguyên tố cùng nhau
=> điều cần CM