Question

[Tống Thùy Linh]

Ai đó giúp mik giải Toán hình học đc ko ạ !
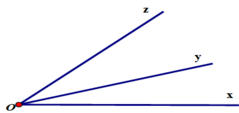
Trên cùng một nửa mặt phẳng bờ chứa tia Ox,vẽ hai tia Oy,Oz sao cho \(\widehat{xOy}=65^o;\widehat{xOz}=130^o\)
a) Trong ba tia Ox,Oy,Oz tia nào nằm giữa hai tia còn lại ? Vì sao ?
b) Tính số đo \(\widehat{yOz}\)
c) So sánh \(\widehat{xOy}\)và \(\widehat{yOz}\)
d) Vẽ tia Om là tia đối của tia Ox.Tính \(\widehat{yOm}\)
Cho hai góc \(\widehat{xOm}\)và \(\widehat{yOm}\)là hai góc kề bù.Biết \(\widehat{xOm}=80^o\),tính \(\widehat{yOm}\)
Mn giúp mik giải vs mai mik nộp bài rùi :))
Mik ko ra điều kiện có khó nhưng giải hình ra còn ko giải ra đc thì ko sao
 

Answer 1

[_Lương Linh_]

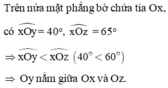
Lời giải bài 1:

Answer 2

[Nguyễn Thị Thúy Hường]

\(\text{a) Trên cùng 1 nửa mặt phẳng bờ chứa tia Ox có}\)\(\widehat{xOy}< \widehat{xOz}\) \(\left(65< 130\right)\)

    \(\Rightarrow\text{ Oy nằm giữa Ox và Oz}\)

b) \(\text{Do Oy nằm giữa Ox và Oz }\)

\(\Rightarrow\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\Rightarrow\widehat{xOz}-\widehat{xOy}=\widehat{yOz}\left(1\right)\)

  mà \(\widehat{xOy}=65^0;\widehat{xOz}=130^0\left(2\right)\)

\(\text{Từ (1) và (2)}\)\(\Rightarrow\)\(\widehat{yOz}=130^0-65^0=65^0\)

\(c.\)

Ta thấy \(\widehat{xOy}=65^0;\widehat{yOz}=65^0\)

\(\Rightarrow\widehat{xOy}=\widehat{yOz}\)

\(\text{d}.\)\(\widehat{yOm}+\widehat{xOy}=180^0\) \(\text{(kề bù)}\)

\(\Rightarrow\widehat{yOm}=\widehat{180^0}-\widehat{xOy}\left(3\right)\)

\(\text{ mà }\)\(\widehat{xOy}=65^0\)

\(\Rightarrow\widehat{yOm}=180^0-65^0=125^0\)

   \(\widehat{xOm}+\widehat{yOm}=180^0\) \(\text{(kề bù)}\)

\(\Rightarrow\widehat{yOm}=180^0-\widehat{xOm}\)

\(\text{mà }\)\(\widehat{xOm}=80^0\)

\(\Rightarrow\widehat{yOm}=100^0\)