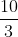Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a)(2x+1)(3x-2)=(5x-8)(2x+1)
⇔(2x+1)(3x-2)-(5x-8)(2x+1)=0
⇔(2x+1)(3x-2-5x+8)=0
⇔(2x+1)(-2x+6)=0
⇔2x+1=0 hoặc -2x+6=0
1.2x+1=0⇔2x=-1⇔x=-1/2
2.-2x+6=0⇔-2x=-6⇔x=3
phương trình có 2 nghiệm x=-1/2 và x=3
`a,(x+3)(x^2+2021)=0`
`x^2+2021>=2021>0`
`=>x+3=0`
`=>x=-3`
`2,x(x-3)+3(x-3)=0`
`=>(x-3)(x+3)=0`
`=>x=+-3`
`b,x^2-9+(x+3)(3-2x)=0`
`=>(x-3)(x+3)+(x+3)(3-2x)=0`
`=>(x+3)(-x)=0`
`=>` $\left[ \begin{array}{l}x=0\\x=-3\end{array} \right.$
`d,3x^2+3x=0`
`=>3x(x+1)=0`
`=>` $\left[ \begin{array}{l}x=0\\x=-1\end{array} \right.$
`e,x^2-4x+4=4`
`=>x^2-4x=0`
`=>x(x-4)=0`
`=>` $\left[ \begin{array}{l}x=0\\x=4\end{array} \right.$
1) a) \(\left(x+3\right).\left(x^2+2021\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\x^2+2021=0\end{matrix}\right.\\\left[{}\begin{matrix}x=-3\left(nhận\right)\\x^2=-2021\left(loại\right)\end{matrix}\right. \)
=> S={-3}
a) \(9x^2-1=\left(3x+1\right)\left(2x-1\right)\)
\(\Rightarrow\left(3x+1\right)\left(3x-1\right)=\left(3x+1\right)\left(2x-1\right)\)
\(\Leftrightarrow\left(3x+1\right)\left(3x-1\right)-\left(3x+1\right)\left(2x-1\right)=0\)
\(\Leftrightarrow\left(3x+1\right)\left(3x-1-2x+1\right)=0\)
\(\Leftrightarrow x\left(3x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\3x+1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{-1}{3}\end{cases}}\)
b) \(\left(4x-3\right)^2=4\left(x^2-2x+1\right)\)
\(\Leftrightarrow16x^2-24x+9=4x^2-8x+4\)
\(\Leftrightarrow12x^2-16x+5=0\)
Ta có \(\Delta=16^2-4.12.5=16,\sqrt{\Delta}=4\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{16+4}{12}=\frac{5}{3}\\x=\frac{16-4}{12}=1\end{cases}}\)
1. 3x( x - 2 ) - ( x - 2 ) = 0
<=> ( x-2).(3x-1) = 0 => x = 2 hoặc x = \(\dfrac{1}{3}\)
2. x( x-1 ) ( x2 + x + 1 ) - 4( x - 1 )
<=> ( x - 1 ).( x (x^2 + x + 1 ) - 4 ) = 0
(phần này tui giải được x = 1 thôi còn bên kia giải ko ra nha )
3 \(\left\{{}\begin{matrix}\sqrt{5}x-2y=7\\\sqrt{5}x-5y=10\end{matrix}\right.\)<=> \(\left\{{}\begin{matrix}y=-1\\x=\sqrt{5}\end{matrix}\right.\)
\(1. 3x^2 - 7x +2=0\)
=>\(Δ=(-7)^2 - 4.3.2\)
\(= 49-24 = 25\)
Vì 25>0 suy ra phương trình có 2 nghiệm phân biệt:
\(x_1\)=\(\dfrac{-\left(-7\right)+\sqrt{25}}{2.3}=\dfrac{7+5}{6}=2\)
\(x_2\)=\(\dfrac{-\left(-7\right)-\sqrt{25}}{2.3}=\dfrac{7-5}{6}=\dfrac{1}{3}\)
a) (3x2 - 7x – 10)[2x2 + (1 - √5)x + √5 – 3] = 0
=> hoặc (3x2 - 7x – 10) = 0 (1)
hoặc 2x2 + (1 - √5)x + √5 – 3 = 0 (2)
Giải (1): phương trình a - b + c = 3 + 7 - 10 = 0
nên
x1 = - 1, x2 =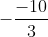
= 
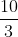
Giải (2): phương trình có a + b + c = 2 + (1 - √5) + √5 - 3 = 0
nên
x3 = 1, x4 =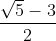
b) x3 + 3x2– 2x – 6 = 0 ⇔ x2(x + 3) – 2(x + 3) = 0 ⇔ (x + 3)(x2 - 2) = 0
=> hoặc x + 3 = 0
hoặc x2 - 2 = 0
Giải ra x1 = -3, x2 = -√2, x3 = √2
c) (x2 - 1)(0,6x + 1) = 0,6x2 + x ⇔ (0,6x + 1)(x2 – x – 1) = 0
=> hoặc 0,6x + 1 = 0 (1)
hoặc x2 – x – 1 = 0 (2)
(1) ⇔ 0,6x + 1 = 0
⇔ x2 =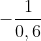
= 
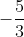
(2): ∆ = (-1)2 – 4 . 1 . (-1) = 1 + 4 = 5, √∆ = √5
x3 =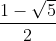
, x4 =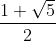 
Vậy phương trình có ba nghiệm:
x1 =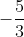
, x2 = 
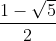, x3 = 
,
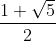d) (x2 + 2x – 5)2 = ( x2 – x + 5)2 ⇔ (x2 + 2x – 5)2 - ( x2 – x + 5)2 = 0
⇔ (x2 + 2x – 5 + x2 – x + 5)( x2 + 2x – 5 - x2 + x - 5) = 0
⇔ (2x2 + x)(3x – 10) = 0
⇔ x(2x + 1)(3x – 10) = 0
Hoặc x = 0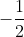, x =
, x =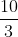 
Vậy phương trình có 3 nghiệm:
x1 = 0, x2 =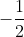
, x3 = 