Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Áp dụng hệ thức giữa cạnh và đường cao trong các tam giác vuông

∆AHC và ∆AHB ta có:
AE.AC = A H 2 = AD.AB => ∆AHC ~ ∆AHB(c.g.c)
b. Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ∆ABC tính được AH = 3cm => DE = 3cm
Trong ∆AHB vuông ta có:
tan A B C ^ = A H H B => A B C ^ ≈ 56 0 , S A D E = 27 13 c m 2

2)
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow DE^2=2\cdot4.5=9\)
hay DE=3(cm)
b) Xét ΔABH vuông tại H có
\(\tan\widehat{ABC}=\dfrac{AH}{HB}=\dfrac{3}{2}\)
nên \(\widehat{ABC}\simeq56^0\)

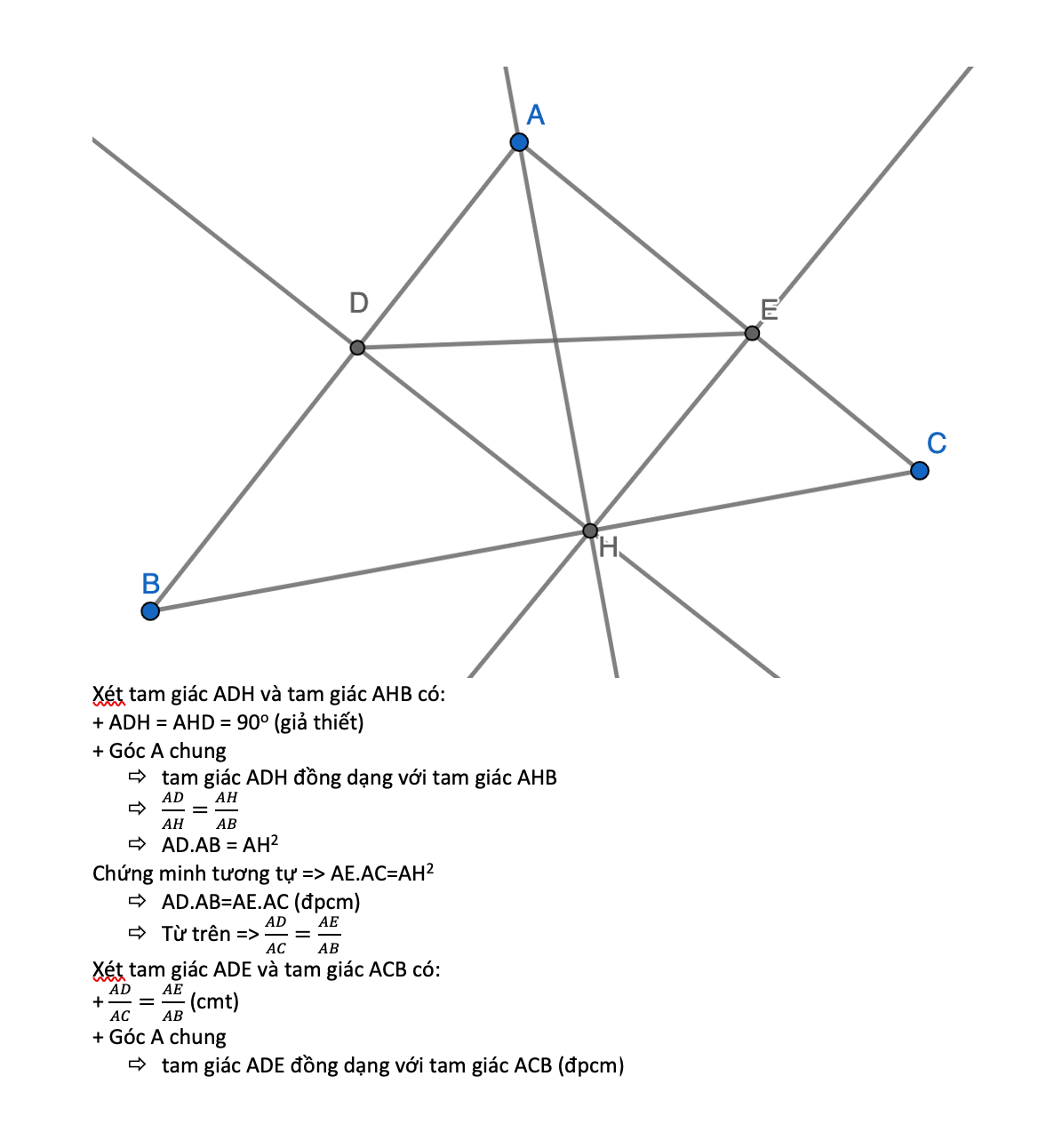
a, Xét ΔABH và ΔAHD có
Góc A chung
Góc ADH=Góc AHB=90°
=> ΔABH ~ΔAHD(g.g)
=> AH/AB=AD/AH
=> AB.AD=AH²(1)
Xét ΔAEH và ΔAHC có:
Góc A chung
Góc AEH = góc AHC
=>ΔAEH~ΔAHC(g.g)
=> AE/AH=AH/AC
=>AE.AC=AH²(2)
Từ (1);(2) => AD.AB=AE.AC(đpcm)
b, vì ΔABC vuông tại A có AI là trung tuyến ứng với cạnh huyền=> BI=IC=AI
=> ΔAIC cân tại I
=>góc IAC =góc ICA
Ta cũng có ΔBIA cân tại I =>góc IBA=góc BAI
Mà góc BAI =góc AED(cùng phụ)
=> góc IBA=góc AED
Mà ABI+góc ACI= 90°
=> gócAED + góc IAC=90°
=> DEvuông góc vs AI
c,
mình làm câu c,d nek bạn
c, ta có\(\Delta\)HEC vuông tại E( vì E là hình chiếu của H nên Góc E=90 độ)
=> EN là đường trung tuyến ứng vs cạnh huyền
=> EN=NH=NC( vì N là trung điểm của HC)
=> \(\Delta\)ENC cân tại N(NE=NC cmt)
=> góc NEC=góc NCE(hai góc đáy) (1)
chứng minh tương tự trong \(\Delta\)BMD cân tại M
=> góc DBM=góc MDB(2)
ta có \(\Delta\)ABC vuông tại A nên góc DBM+góc NCE=90 độ
=>góc MDB+ góc NEC(vì (1);(2)) (3)
và \(\Delta\)\(\Delta\)
DAE vuông tại A nên góc ADE+góc AED=90 độ (4)
từ (3);(4)=>góc BDM+góc ADE=90 độ
=> góc MDH+góc HDE=90 độ ( 180 độ - (MDH+HDE))
=> DM\(\perp\) DE (*)
và góc DEA+ góc NEC=90 độ
=> góc HDE+góc HEN= 90 độ
=> DE\(\perp\) EN (**)
từ (*); (**)=> MDEN là hình thang (DM // EN vì cùng \(\perp\)vs DE)
d, Ta có DHEA là hình chữ nhật (góc D= góc H =Góc E=90 độ)
=> OH=OA=OD=OE (t/c đường chéo hcn)
=> OH=OA=HA/2
ta có HM+HN=BM+NC(vì BM=MH; NH=NC)
=> MH+HN=BC/2=>MN=1/2 BC
diện tích \(\Delta\)ABC =1/2. AH. BC
diện tích \(\Delta\)MON=1/2.OH.MN=1/2.1/2AH.1/2BC
Vậy (S\(\Delta\) MON)/(S\(\Delta\)ABC)=(1/2.AH.BC)/(1/8 AH.BC)
=4
Mình nghĩ là làm như vậy, có gì bạn góp ý nha![]()

a.
\(AB^2+AC^2=4,5^2+6^2=56,25\)
\(BC^2=7,5^2=56,25\)
\(\Rightarrow AB^2+AC^2=BC^2\Rightarrow\Delta ABC\) vuông tại A theo Pitago đảo
b.
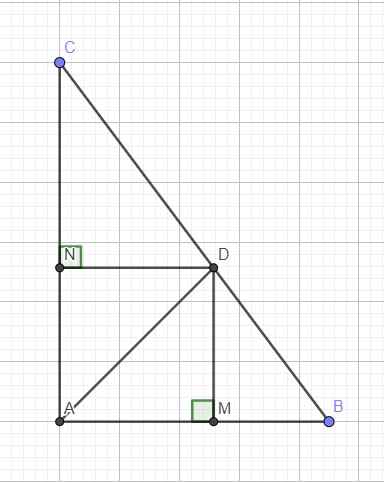
Theo định lý phân giác: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow DB=\dfrac{3}{4}DC\)
Mà \(DB+DC=BC=7,5\)
\(\Rightarrow\dfrac{3}{4}DC+DC=7,5\Rightarrow DC=\dfrac{30}{7}\left(cm\right)\)
Do DN và AB cùng vuông góc AC \(\Rightarrow DN||AB\)
Áp dụng định lý Talet:
\(\dfrac{DN}{AB}=\dfrac{DC}{BC}=\dfrac{4}{7}\Rightarrow DN=\dfrac{4}{7}AB=\dfrac{18}{7}\left(cm\right)\)
Tứ giác AMDN là hình chữ nhật (có 3 góc vuông)
Mà AD là đường chéo đồng thời là phân giác theo giả thiết
\(\Rightarrow AMDN\) là hình vuông
\(\Rightarrow S_{AMDN}=DN^2=\dfrac{324}{49}\approx6,6\left(cm^2\right)\)

b: Xét ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

b: Xét ΔAHB vuông tại H có HD là đường cao ứng với cạnh huyền AB
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
hay \(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét ΔADE vuông tại A và ΔACB vuông tại A có
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Do đó: ΔADE\(\sim\)ΔACB
Suy ra: \(\widehat{ADE}=\widehat{ACB}\)