Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Đạo hàm y’ = x2- mx+ 2m
Hàm số nghịch biến trên một đoạn có độ dài là 3 khi và chi khi phương trình y’ =0 có 2 nghiệm x1; x2 ( chú ý hệ số a= 1> 0) thỏa mãn:
x 1 - x 2 = 3 ⇔ ∆ > 0 ⇔ m 2 - 8 m > 0 ( x 1 - x 2 ) 2 = 9 ⇔ S 2 - 4 P = 9 ⇔ m > 8 h a y m < 0 m 2 - 8 m = 9
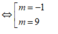
Chọn A.

Chọn A.
Tập xác định: D = R. Ta có ![]()
Ta không xét trường hợp y' ≤ 0, ∀ x ∈ R vì a = 1> 0.
Hàm số nghịch biến trên một đoạn có độ dài là 3 ⇔ y' = 0 có 2 nghiệm x1; x2 thỏa mãn:
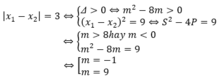

Chọn A
Ta có ![]() .
.
Đặt ![]() , xét hàm
, xét hàm ![]() ,
, ![]() .
.
Hàm số nghịch biến trên ![]() khi
khi ![]() .
.
![]() ,
,![]() .
.
Xét hàm ![]() ,
, ![]() .
.
Ta có ![]() ,
, ![]() .
.
Lập bảng BBT trên ![]() , ta có
, ta có ![]() thỏa YCBT
thỏa YCBT

Chọn A
Phương pháp:
Tính y'.
Điều kiện để hàm số đã cho nghịch biến trên - ∞ ; 1 là
Cách giải:
Tập xác định ![]()
Ta có 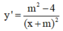
Để hàm số nghịch biến trên khoảng
-
∞
;
1
![]()


Chọn A.
Ta có: ![]()
Hàm số đã cho nghịch biến trên [1;+ ∞ )khi và chỉ khi
![]()
![]()
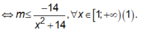
Đặt 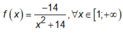
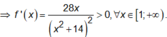
Do đó: 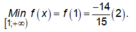
Từ (1), (2) suy ra giá trị m cần tìm là: 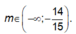
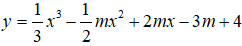

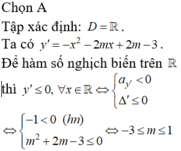


\(y'=x^2-mx+2m=0\) (1)
Hàm nghịch biến trên một đoạn có độ dài bằng 3 khi và chỉ khi:
\(\left\{{}\begin{matrix}\Delta=m^2-8m>0\\\left|x_1-x_2\right|=3\\\end{matrix}\right.\) trong đó \(x_1;x_2\) là 2 nghiệm của (1)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 0\\m>8\end{matrix}\right.\\\left(x_1+x_2\right)^2-4x_1x_2=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 0\\m>8\end{matrix}\right.\\m^2-8m=9\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=-1\\m=9\end{matrix}\right.\)
y′=x2−mx+2m=0 (1)
Hàm nghịch biến trên một đoạn có độ dài bằng 3 khi và chỉ khi:
{Δ=�2−8�>0∣�1−�2∣=3{Δ=m2−8m>0∣x1−x2∣=3 trong đó �1;�2x1;x2 là 2 nghiệm của (1)
⇔{[�<0�>8(�1+�2)2−4�1�2=9⇔⎩⎨⎧[m<0m>8(x1+x2)2−4x1x2=9
⇔{[�<0�>8�2−8�=9⇔⎩⎨⎧[m<0m>8m2−8m=9 ⇒[�=−1�=9⇒[m=−1m=9