K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

7 tháng 5 2020
Bạn ơi, bài này sai đề r, phải là gọi H,K lần lượt lầ hc của I trên AB,BC!

8 tháng 5 2015
bạn tự vẽ hình nha
trên tia đối cũa tia ad ,,vẽ tia at,trên tia at vẽ điểm n sao cho an =ak
bad =cad =120 độ chia 2 = 60 độ
suy ra góc bad =cad= nai = 6o độ (2 góc đối đỉnh)
góc bac +cai =180 độ mà bac =120 độ nên cai = 60 độ
nên góc nai bằng kai
cmd tam giac nai =kai (c.g.c) nên góc ani=aki = 90 độ và in=ik (2ctu)
cmd tam giac dni=dei (ch.gn)suy ra in =ie
từ 2 điều trên suy ra ik =ie


A. Ta có: $\angle BAD=\angle CAD$ $\angle ADB=120^{\circ}-\angle BAD=120^{\circ}-\angle CAD =$ $\angle ACD$ Vậy $AD$ là phân giác trong của $\angle A$ trong tam giác $ABC$ Do đó ta có $\frac{BD}{DC}=\frac{AB}{AC}$ (định lí phân giác) Mà $\angle A=\angle AHD$ (Do $H$ thuộc đường thẳng $AC$ là đường cao của tam giác $ABD$) $\angle HDA=180^{\circ}-\angle BDA=180^{\circ}-\angle B=120^{\circ}=\angle C$ Vậy $\frac{HD}{DC}=\frac{AD}{AC}=\frac{AB}{AC}=\frac{BD}{DC}$ Vậy $HD=BD$ và $\angle B=60^{\circ}=\angle HAD$ Do đó $\triangle AHD \cong \triangle ABD$ Vậy $\triangle ABC \cong \triangle AHD$ B. Ta có $\angle ADB=120^{\circ}-\angle BAD=120^{\circ}-\angle DAC=\angle ACD$ Lại có $AD$ là phân giác trong của $\angle A$ Do đó, ta có: $\frac{BD}{DC}=\frac{AB}{AC}=\frac{BD}{DA}$ Vậy $DC=DA$, vậy $AD$ là đường trung trực của $BH$ C. Ta có $\angle AHD = \angle B = 60^{\circ}=\angle HAC$, vậy $\triangle AHD \sim \triangle ACH$ Do đó $\dfrac{HA}{HD}= \dfrac{HC}{HA}$ Vậy $HA=HC$ D. Ta có $\angle ADB=120^{\circ}-\angle BAD=120^{\circ}-\angle DAC=\angle ACD$ Do đó tam giác $ABC$ cân tại $B$, ta có $DC>AB$ (Bất đẳng thức tam giác) E. Gọi $E$ là trung điểm của $CS$ thì ta có $CE=\frac{1}{2}CS$ Mà $\angle ACB=\angle AHB=90^{\circ}$, do đó $AH//CB$, ta có $\triangle AHB \sim \triangle ACB$ Vậy $\dfrac{AB}{AC}=\dfrac{HB}{BC}$ Do đó $\dfrac{HB}{AB}=\dfrac{BC}{AC}$ Vì $HEBC$ là hình bình hành nên ta có $BC=HE$ Vậy $\dfrac{HB}{AB}=\dfrac{HE}{AC}$ Lại có $\triangle HSD \sim \triangle AHC$ Vậy $\dfrac{HS}{AC}=\dfrac{HD}{AH}$ Do đó $\dfrac{HE}{AC}=\dfrac{HD+DE}{AC}=\dfrac{HD}{AC}+\dfrac{DE}{AC}$ Vì $HA=HC$ nên ta có $HD=\frac{1}{2}AC$ Vậy $\dfrac{HE}{AC}=\dfrac{1}{2}+\dfrac{DE}{AC}$ Mà $HE=\frac{1}{2}CS=\frac{1}{4}AB$ nên $\dfrac{HE}{AB}=\dfrac{1}{4}$ Do đó $\dfrac{1}{2}+\dfrac{DE}{AC}=\dfrac{1}{4}$ Vậy $\dfrac{DE}{AC}=-\dfrac{1}{4}$ Ta có $\triangle BDS \sim \triangle ACS$ Vậy $\dfrac{BD}{AC}=\dfrac{DS}{CS}$ Mà $\angle B =\angle HAD=60^{\circ} =\angle SDC$ Nên tam giác $SDC$ cũng là tam giác đều với $SD=DC$ Vậy $\dfrac{BD}{AC}=\dfrac{DS}{CS}=\dfrac{1}{2}$ Do đó $DE=\frac{-1}{4}AC$, suy ra $DE$ song song với $AC$ Lại có $\angle AHB=90^{\circ}$ nên $BH$ vuông góc với $AC$ Do đó $AD$ là đường trung trực của $BH$ nên $DE$ cũng là đường trung trực của $BH$ Vậy ta được $A,D,E$ thẳng hàng Chúc bạn học tốt!
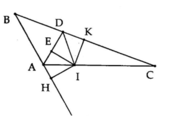
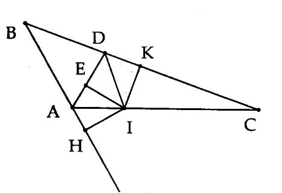
Kẻ ��⊥��IE⊥AD (với �∈��E∈AD).
Gọi ��Ax là tia đối của tia ��AB.
Vì ���^BAC và ���^CAx là hai góc kề bù mà ���^=120∘BAC=120∘ nên ���^=60∘CAx=60∘ (1)
Ta có ��AD là phân giác của ���^⇒���^=12���^=60∘BAC⇒DAC=21BAC=60∘ (2)
Từ (1) và (2) suy ra ��AC là tia phân giác của ���^DAx
⇒��=��⇒IH=IE (tính chất tia phân giác của một góc) (3)
Vì ��DI là phân giác của ���^ADC nên ��=��IK=IE (tính chất tia phân giác của một góc) (4)
Từ (3) và (4)(4) suy ra ��=��IH=IK.