Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là B
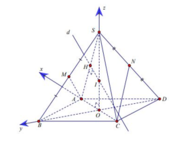
Chọn hệ trục tọa độ Oxyz như hình vẽ, ta có:
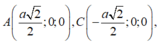
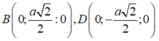
Đặt SO = x > 0. => S (0;0; x).
M , N lần lượt là trung điểm của SB và SD nên:
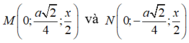
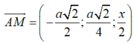
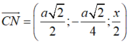
Theo giả thiết: AM ⊥CN
![]()
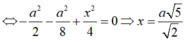
SO là trục đường tròn ngoại tiếp mặt đáy.
Gọi H là trung điểm SA . Qua H dựng đường trung trực d của SA, I= d ∩ SO .
=> Mặt cầu ngoại tiếp khối chóp S .ABCD có tâm I , bán kính R = SI.
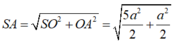
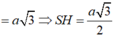
∆ SHI đồng dạng với ∆ SOA

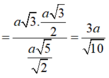
Vậy bán kính mặt cầu ngoại tiếp khối chóp S ABCD . là R= 3 a 10

Đáp án B
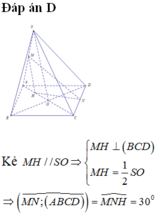
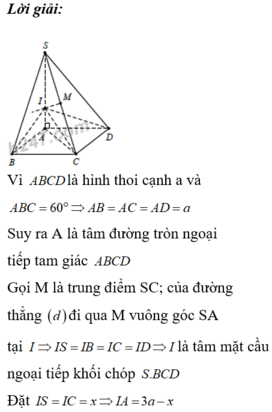
Do các cạnh bên bằng nhau nên hình chiếu của S lên (ABCD) phải trùng với tâm H của hình vuông ABCD.
Dễ thấy I là trung điểm của SC, vì BD ⊥ SC, nên BD//(P). Do đó EF // BD. Để ý rằng EF đi qua trọng tâm J của tam giác SDB.
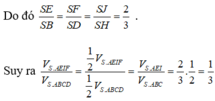
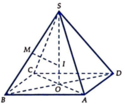



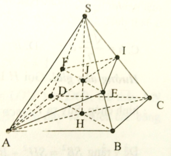
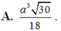
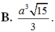
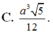
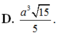
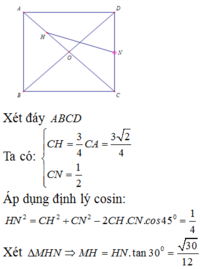

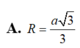
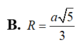

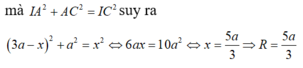
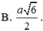
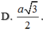

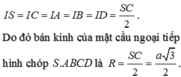
a) \(O\) là giao điểm của hai đường chéo của hình vuông \(ABCD\).
\(OC=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{2}AB=\dfrac{a\sqrt{2}}{2}\)
\(SO=\sqrt{SC^2-OC^2}=\sqrt{\left(a\sqrt{2}\right)^2-\left(\dfrac{a\sqrt{2}}{2}\right)^2}=\dfrac{a\sqrt{6}}{2}\).
\(V_{S.ABCD}=\dfrac{1}{3}.SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{a\sqrt{6}}{2}.a^2=\dfrac{a^3\sqrt{6}}{6}\)
b) Gọi \(I\) là tâm mặt cầu ngoại tiếp hình chóp \(S.ABCD\).
Khi đó \(IA=IS\)
\(\Leftrightarrow\sqrt{OA^2+OI^2}=SO-OI\)
\(\Leftrightarrow\sqrt{\dfrac{a^2}{2}+OI^2}=\dfrac{a\sqrt{6}}{2}-OI\)
\(\Leftrightarrow\dfrac{a^2}{2}+OI^2=\left(\dfrac{a\sqrt{6}}{2}-OI\right)^2\)
\(\Leftrightarrow OI=\dfrac{a\sqrt{6}}{6}\).
Suy ra bán kính mặt cầu ngoại tiếp hình chóp \(S.ABCD\) là
\(SI=SO-OI=\dfrac{a\sqrt{6}}{2}-\dfrac{a\sqrt{6}}{6}=\dfrac{a\sqrt{6}}{3}\).
c) \(A'C'//AC\) suy ra \(A'C'\) vuông góc với mặt phẳng \(\left(SBD\right)\).
Mà \(A'C'\) cắt \(\left(SBD\right)\) tại trung điểm của nó nên \(C'\) đối xứng với \(A'\) qua mặt phẳng \(\left(SBD\right)\).
Tương tự \(A\) đối xứng với \(C\) qua mặt phẳng \(\left(SBD\right)\).
Suy ra phép đối xứng qua mặt phẳng \(\left(SBD\right)\) biến hình chóp \(A'.ABCD\) thành hình chóp \(C'.CBAD\) do đó hai hình chóp đó bằng nhau.