TN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
15 tháng 4 2019
(a + b)(a + b) = a(a + b) + b(a + b)
= a2 + ab + ba + b2
= a2 + 2ab + b2
CM
4 tháng 12 2019
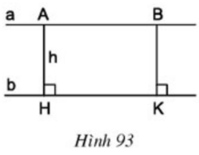
AH // BK (cùng ⊥ b) và AB // HK ⇒ tứ giác ABKH là hình bình hành
⇒ AH = BK = h
HP
1
HP
2
18 tháng 6 2017
Giả sử : a là số chẵn, b là số lẻ
Ta có : a . b = chẵn . lẻ = chẵn → Cho dù a + b là số nào đi nữa thì ab ( a+ b ) vẫn là số chẵn ( vì ab = số chẵn )
Giả sử : a là số lẻ, b là số lẻ
Ta có : ( a + b ) = lẻ + lẻ = chẵn → Cho dù ab là số nào đi nữa thì ab ( a+ b ) vẫn là số chẵn ( vì ( a + b ) = số chẵn )
18 tháng 6 2017
Bonking thiếu nha bạn
Còn 2 trường hợp nữa
Nếu a là số lẻ b là số chẵn
Thì ab là số chẵn => ab(a + b) cũng là số chẵn
Nếu a là số chẵn , b là số lẻ thì mk chịu
9 tháng 5 2023
3:
Gọi hai số cần tìm lần lượt là a,b
Theo đề, ta có: a=2b và a-b=22
=>b=22; a=44
19 tháng 4 2022
Ta có:
\(\left(a-1\right)^2\ge0;\forall a\) (1)
\(\left(b-1\right)^2\ge0;\forall b\) (2)
\(\left(c-1\right)^2\ge0;\forall c\) (3)
Cộng từng vế (1);(2);(3) ta được:
\(\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2\ge0\)
\(\Leftrightarrow a^2-2a+1+b^2-2b+1+c^2-2c+1\ge0\)
\(\Leftrightarrow a^2+b^2+c^2-2\left(a+b+c\right)+3\ge0\)
\(\Leftrightarrow a^2+b^2+c^2+3\ge2\left(a+b+c\right)\) ( đfcm )
PT
19 tháng 4 2022
Ta có:
(a−1)2≥0;∀a(a−1)2≥0;∀a (1)
(b−1)2≥0;∀b(b−1)2≥0;∀b (2)
(c−1)2≥0;∀c(c−1)2≥0;∀c (3)
Cộng từng vế (1);(2);(3) ta được:
(a−1)2+(b−1)2+(c−1)2≥0(a−1)2+(b−1)2+(c−1)2≥0
⇔a2−2a+1+b2−2b+1+c2−2c+1≥0⇔a2−2a+1+b2−2b+1+c2−2c+1≥0
⇔a2+b2+c2−2(a+b+c)+3≥0⇔a2+b2+c2−2(a+b+c)+3≥0
⇔a2+b2+c2+3≥2(a+b+c)⇔a2+b2+c2+3≥2(a+b+c) ( đpcm ).
9 tháng 11 2016
Giả sử BĐT trên đúng
Ta có \(\frac{a^2}{x}+\frac{b^2}{y}>=\frac{\left(a+b\right)^2}{x+y}\\
\Leftrightarrow\frac{a^2y+b^2x}{xy}\ge\frac{\left(a+b\right)^2}{x+y}\\
\Leftrightarrow\left(a^2y+b^2x\right)\left(x+y\right)\ge\left(a+b\right)^2xy\)
Bạn nhân ra rồi thu gọn tất cả các hạng tử về vế trái rồi được hàng đẳng thức:
\(\left(ay-bx\right)^2\ge0\) (luôn đúng)
Vậy BĐT đúng
Cách 1 : Dựa vào lập phương của 1 tổng
Cách 2 : Nhân đa thức với đa thức