Phần tự luận (5 điểm) SVIP

Hướng dẫn giải:

Tập xác định: $D=\mathbb{R}$.

Ta có $f(1)={{1}^{2}}+m.1=m+1$.

$\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f(x)=\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,({{x}^{2}}+mx)=m+1$;

$\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,f(x)=\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,\dfrac{\sqrt{x+3}-2}{x-1}=\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,\dfrac{(x+3)-{{2}^{2}}}{(x-1)\left( \sqrt{x+3}+2 \right)}$ $=\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,\dfrac{x-1}{(x-1)\left( \sqrt{x+3}+2 \right)}=\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,\dfrac{1}{\sqrt{x+3}+2}=\dfrac{1}{\sqrt{1+3}+2}=\dfrac{1}{4}$.

Hàm số $f(x)$ liên tục tại $x=1$$\Leftrightarrow \underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f(x)=\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,f(x)=f(1)$

$\Leftrightarrow m+1=\dfrac{1}{4}$ $\Leftrightarrow m=-\dfrac{3}{4}$.

Vậy $m=-\dfrac{3}{4}$ là giá trị cần tìm.

Hướng dẫn giải:

Ta có: ${f}'\left( x \right)={{x}^{2}}+2\left( m-1 \right)x-\left( 2m-10 \right)$

${f}'\left( x \right)>0\,,\,\forall x\in \mathbb{R}\,\Leftrightarrow \,{{x}^{2}}+2\left( m-1 \right)x-\left( 2m-10 \right)>0\,,\,\forall x\in \mathbb{R}$

$\Leftrightarrow \,\left\{ \begin{aligned} & a=1>0 \\ & {\Delta }'={{\left( m-1 \right)}^{2}}+\left( 2m-10 \right)<0 \\ \end{aligned} \right.$

$\Leftrightarrow \,{{m}^{2}}-9<0$ $\Leftrightarrow \,-3<m<3$.

Vậy $m\,\in \,\left( -3\,;\,3 \right)$ thì ${f}'\left( x \right)>0\,,\,\forall x\in \mathbb{R}$.

Hướng dẫn giải:

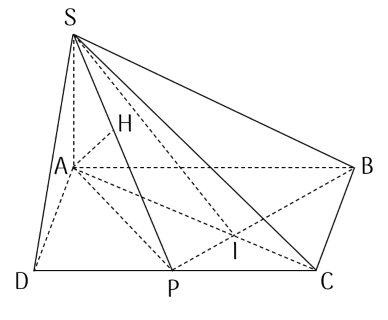
a) Ta có: $\left\{ \begin{aligned} & \left( SAB \right)\bot \left( ABCD \right) \\ & \left( SAD \right)\bot \left( ABCD \right) \\ & \left( SAB \right)\cap \left( SAD \right)=SA \\ \end{aligned} \right.\Rightarrow SA\bot \left( ABCD \right)$

b) Ta có $\left\{ \begin{aligned} & SI\cap \left( ABCD \right)=I \\ & SA\bot \left( ABCD \right) \\ \end{aligned} \right.\,\Rightarrow \,$ $AI$ là hình chiếu của $SI$ trên mặt phẳng $\left( ABCD \right)$.

$\Rightarrow $ góc giữa $SI$ và mặt phẳng $\left( ABCD \right)$ là $\widehat{SIA}$ (vì  $\widehat{SIA}$ nhọn).

Có $CP\,//\,AB\,\Rightarrow \,\dfrac{CP}{AB}=\dfrac{CI}{AI}=\dfrac{1}{2}$.

Vì $CA\cap \left( SBP \right)=I$ $\Rightarrow \,\dfrac{{d}\left( C,\left( SBP \right) \right)}{{d}\left( A,\left( SBP \right) \right)}=\dfrac{CI}{AI}=\dfrac{1}{2}$

$\Rightarrow \, {d}\left( A,\left( SBP \right) \right)=2{d}\left( C,\left( SBP \right) \right)=a$.

Mà $BP=\sqrt{B{{C}^{2}}+C{{P}^{2}}}=a\sqrt{2}\,,\,AP=\sqrt{A{{D}^{2}}+D{{P}^{2}}}=a\sqrt{2}$ và $AB=2a$.

$\Rightarrow \,\Delta APB$ vuông tại $P$.

Kẻ $AH$ vuông góc với $SP$ tại $H$.

Ta có $\left. \begin{aligned}  \left. \begin{aligned} & BP\bot AP \\ & BP\bot SA \\ \end{aligned} \right\} \,\Rightarrow \,BP\bot \left( SAP \right)\,\Rightarrow \,BP\bot AH \\  SP\bot AH \\ \end{aligned} \right\} \,\Rightarrow AH\bot \left( SBP \right)$.

Suy ra $AH$ là khoảng cách từ $A$ đến mặt phẳng $\left( SBP \right)$ và $AH=a$.

Xét tam giác $SAP$ vuông tại $A$ có $\dfrac{1}{A{{H}^{2}}}=\dfrac{1}{S{{A}^{2}}}+\dfrac{1}{A{{P}^{2}}}\,\Rightarrow \,\dfrac{1}{S{{A}^{2}}}=\dfrac{1}{A{{H}^{2}}}-\dfrac{1}{A{{P}^{2}}}=\dfrac{1}{2{{a}^{2}}}$.

$\Rightarrow \,SA=a\sqrt{2}$.

Mà $AI=\dfrac{2}{3}AC=\dfrac{2a\sqrt{5}}{3}$.

Trong tam giác $SAI$ vuông tại $A$ có $\tan \widehat{SIA}=\dfrac{SA}{AI}=\dfrac{a\sqrt{2}}{\dfrac{2a\sqrt{5}}{3}}=\dfrac{3\sqrt{10}}{10}$.

Vậy góc giữa $SI$ và $\left( ABCD \right)$ là $\widehat{SIA}$ thỏa mãn $\tan \widehat{SIA}=\dfrac{3\sqrt{10}}{10}$.