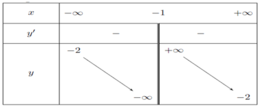
Cho biết bảng biến thiên ở hình dưới là của một trong bốn hàm số được liệt kê dưới đây. Hãy tìm hàm số đó.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Đồ thị hàm số có tiệm cận ngang là y = -1 nên loại A.
Hàm số nghịch biến trên tập xác định của nó nên y' < 0 với x ≠ 1.
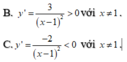
![]()
Suy ra đáp án đúng là C.

Chọn C.
[Phương pháp tự luận]
Nhìn vào bảng biến thiên ta thấy ngay tiệm cận đứng x = 1 , tiệm cận ngang y = - 1 . suy ra loại đáp án A.
Nhìn vào bảng biến thiên , hàm số nghịch biến trên các khoảng - ∞ ; 1 và 1 ; + ∞ .
y = - x - 2 x - 1 có a d - b c = 3 > 0 . Loại đáp án B. y = - x - 3 x - 1 có a d - b c = 4 > 0 . Loại đáp án D. y = - x + 3 x - 1 có a d - b c = - 2 < 0 .
Chọn đáp án C.
[Phương pháp trắc nghiệm]
Nhìn vào bảng biến thiên ta thấy ngay tiệm cận đứng x = 1 , tiệm cận ngang y = - 1
suy ra loại đáp án A.
Nhìn vào bảng biến thiên , hàm số nghịch biến trên các khoảng - ∞ ; 1 và 1 ; + ∞ .
d d x - x - 2 x - 1 x = 0 = 3 > 0 suy ra loại đáp án B.
d d x - x - 3 x - 1 x = 0 = 4 > 0 suy ra loại đáp án D.
d d x - x + 3 x - 1 x = 0 = - 2 < 0 suy ra chọn đáp án C.

Chọn C.
Nhìn vào bảng biến thiên ta thấy ngay tiệm cận đứng x = 1 , tiệm cận ngang y = -1. suy ra loại đáp án A.
Nhìn vào bảng biến thiên, hàm số nghịch biến trên các khoảng ![]()
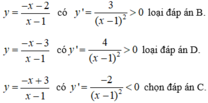

Chọn đáp án C
Từ bảng biến thiên suy ra hệ số của x 3 phải âm nên ta loại phương án A.
Tại x = 0 thì y = -2 suy ra loại C.
y' = 0 có hai nghiệm phân biệt nên loại D.
Do vậy phương án B. thỏa mãn.
Dựa vào BBT ta thấy hàm số có TXĐ: D = R \{-l}, hàm số nghịch biến trên từng khoảng xác định và có
TCN là y = -2.
Ta thấy các hàm số ở cả 4 đáp án đều có TXĐ: D = R \ {-l}.
Tuy nhiên chỉ có đáp án A và đáp án D là đồ thị hàm số có TCN là đường y = -2.
+) Xét đáp án A: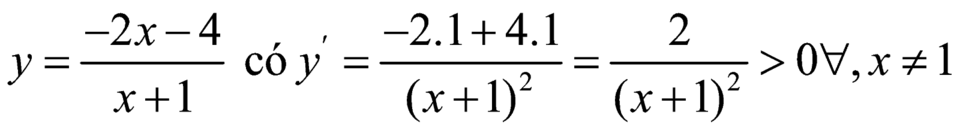 ⇒ hàm số đồng biến trên từng khoảng xác định ⇒ loại đáp án A
⇒ hàm số đồng biến trên từng khoảng xác định ⇒ loại đáp án A
Chọn D