K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
2
27 tháng 7 2021
Ta có: \(\left(2x-8\right)^{2000}+\left(3y+4\right)^{2022}\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-8=0\\3y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=8\\3y=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=-\dfrac{4}{3}\end{matrix}\right.\)
18 tháng 6 2023
M=6x^2+9xy-y^2-5x^2+2xy=x^2+11xy-y^2
(2x-5)^2020+(3y+4)^2022<=0
=>x=5/2 và y=-4/3
M=25/4+11*5/2*(-4/3)-16/9=-1159/36
LB
1
4 tháng 2 2021
\(\left(2x-1\right)^{2020}+\left(y-\frac{2}{5}\right)^{2022}+\left|x+y-z\right|=0\)
Ta có : \(\left(2x-1\right)^{2020}\ge0\forall x;\left(y-\frac{2}{5}\right)^{2022}\ge0\forall x;\left|x+y-z\right|\ge0\forall x;y;z\)
Dấu bằng xảy ra <=> \(x=\frac{1}{2};y=\frac{2}{5};z=x+y=\frac{1}{2}+\frac{2}{5}=\frac{9}{10}\)
Vậy \(x=\frac{1}{2};y=\frac{2}{5};z=\frac{9}{10}\)
KM
1
5 tháng 1 2022
\(a,\left\{{}\begin{matrix}\left|x-3y\right|\ge0\\\left|y+4\right|\ge0\end{matrix}\right.\Rightarrow VT\ge0\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x-3y=0\\y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3y=-12\\y=-4\end{matrix}\right.\)
\(b,Sửa:\left|x-y-5\right|+\left(y+3\right)^2=0\\ \left\{{}\begin{matrix}\left|x-y-5\right|\ge0\\\left(y+3\right)^2\ge0\end{matrix}\right.\Rightarrow VT\ge0\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x-y-5=0\\y+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y+5=2\\y=-3\end{matrix}\right.\)
\(c,\left\{{}\begin{matrix}\left|x+y-1\right|\ge0\\\left(y-2\right)^4\ge0\end{matrix}\right.\Rightarrow VT\ge0\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x+y-1=0\\y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1-y=-1\\y=2\end{matrix}\right.\)
\(d,\left\{{}\begin{matrix}\left|x+3y-1\right|\ge0\\3\left|y+2\right|\ge0\end{matrix}\right.\Rightarrow VT\ge0\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x+3y-1=0\\y+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1-3y=7\\y=-2\end{matrix}\right.\)
\(e,Sửa:\left|2021-x\right|+\left|2y-2022\right|=0\\ \left\{{}\begin{matrix}\left|2021-x\right|\ge0\\\left|2y-2022\right|\ge0\end{matrix}\right.\Rightarrow VT\ge0\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}2021-x=0\\2y-2022=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2021\\y=1011\end{matrix}\right.\)
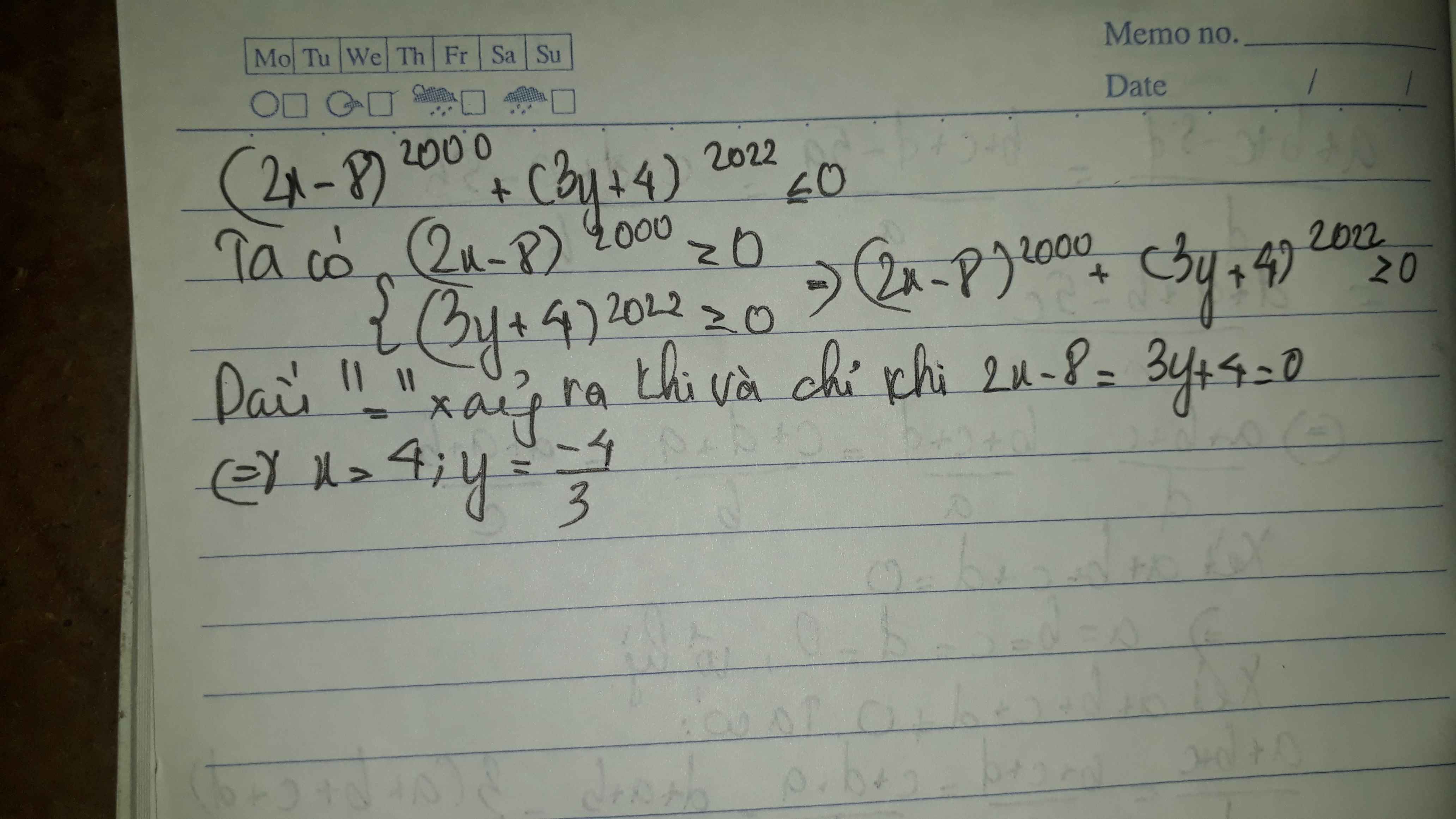
Vì : \(\left(2x-5\right)^{2022}\ge0\forall x,\left(3y+4\right)^{2024}\ge0\forall y\\ =>\left(2x-5\right)^{2022}+\left(3y+4\right)^{2024}\ge0\)
Do đó đề bài xảy ra khi và chỉ khi :
\(\left\{{}\begin{matrix}\left(2x-5\right)^{2022}=0\\\left(3y+4\right)^{2024}=0\end{matrix}\right.\\ =>\left(x;y\right)=\left(\dfrac{5}{2};-\dfrac{4}{3}\right)\)