Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có 3 điểm M ( 8;3 ), N ( 1;4 ), P ( 5;x ) ⇒ M P → - 3 ; x ; - 3 , N P → 4 ; x ; - 4
∆ M N P vuông tại P ⇔ M P → . N P → = 0 ⇔ - 12 + x - 3 x - 4 = 0 ⇔ x = 0 ; x = 7 .
Đáp án B

Đáp án là A.
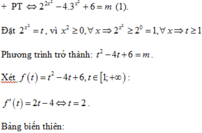
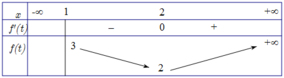
Với t = 1 ⇒ PT (1) có 1 nghiệm x=0.
Với mỗi nghiệm t>1 sẽ sinh ra 2 nghiệm phân biệt khác 0 của phương trình (1).
Để pt (1) có đúng 3 nghiệm m=3.

Đáp án C
Ta có: T = 1 x 1 − 1 x 1 − 3 + 1 x 2 − 1 x 2 − 3 + 1 x 3 − 1 x 3 − 3
T = 1 x 1 − 1 x 1 − 3 + 1 x 2 − 1 x 2 − 3 + 1 x 3 − 1 x 3 − 3 vì 1 x − 1 x − 3 = 1 x − 3 − 1 x − 1 .
Vì x 1 , x 2 , x 3 là 3 nghiệm của phương trình P x = 0 ⇒ P x = x − x 1 x − x 2 x − x 3 .
Suy ra P ' x = x − x 1 x − x 2 + x − x 2 x − x 3 + x − x 3 x − x 1
⇒ P ' x P x = x − x 1 x − x 2 + x − x 3 + x − x 3 x − x 1 x − x 1 x − x 2 x − x 3 = 1 x − x 1 + 1 x − x 2 + 1 x − x 3 * .
Thay x = 1 , x = 3 vào biểu thức (*), ta được T = 1 2 P ' x P 1 − P ' 3 P 3 .

Đáp án C
Điều kiện 4 x 2 − 4 x + 1 2 x > 0 ⇔ x > 0
P T ⇔ log 7 2 x − 1 2 + 2 x − 1 2 = 2 x + log 7 2 x ⇔ f 2 x − 1 2 = f 2 x
với f t = log 7 t + t
f ' t = 1 t ln 7 + 1 > 0 với t >0
→ P T ⇔ 2 x = 2 x − 1 2 ⇔ x = 3 ± 5 4
⇒ x 1 + 2 x 2 = 9 ± 5 4 ⇒ a = 9 b = 5 ⇒ a + b = 14

Chọn B.
Phương pháp:
Giải phương trình bằng phương pháp xét hàm số.
Cách giải:


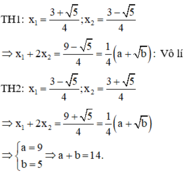
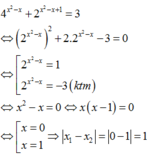

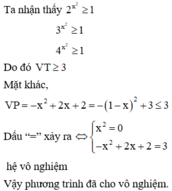
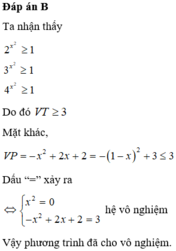
a: \(\Leftrightarrow2x^2+4-x^2+\dfrac{3}{2}=-3+4x^2-\dfrac{4}{3}x^2+1\)
\(\Leftrightarrow x^2+\dfrac{11}{2}=\dfrac{8}{3}x^2-2\)
\(\Leftrightarrow x^2\cdot\dfrac{-5}{3}=-\dfrac{15}{2}\)
\(\Leftrightarrow x^2=\dfrac{9}{2}\)
hay \(x\in\left\{\dfrac{3\sqrt{2}}{2};-\dfrac{3\sqrt{2}}{2}\right\}\)
b: \(\Leftrightarrow\left|x\right|-4-2+\left|x\right|-\dfrac{1}{3}\left|x\right|+5=0\)
\(\Leftrightarrow\left|x\right|\cdot\dfrac{5}{3}=1\)
hay \(x\in\left\{\dfrac{3}{5};-\dfrac{3}{5}\right\}\)