Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Mặt cầu (S) có tâm I (1;0;-2) và bán kính R=2.
Đường thẳng d đi qua điểm N (2; 0; m-1) và có véc tơ chỉ phương 
Điều kiện để d cắt (S) tại hai điểm phân biệt là d (I; (d))<R
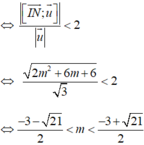
Khi đó, tiếp diện của (S) tại A và B vuông góc với IA và IB nên góc giữa chúng là góc (IA;IB).
Vậy T= {-3;0}. Tổng các phần tử của tập hợp T bằng -3.
Chọn A
Ta có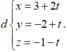 
Vì M là giao điểmcủa d và (P) nên ta có tọa độ của M cũng thỏa mãn phương trình mặt phẳng (P) hay
Gọi điểm H là hình chiếu của M lên
đường thẳng ∆ ta có
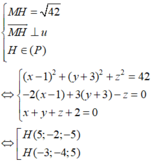
Vậy tồn tại hai đường thẳng ∆ thỏa mãn đề bài
Chọn A
Vì A thuộc 
nên A (1+2t;1-t;-1+t).
Vì B thuộc 
nên B (-2+3t';-1+t';2+2t').
Thay vào (3) ta được t=1, t'=2 thỏa mãn.
A = 1
B = 2
C = 3
Ax + By = Cz = 1 x 8 + 2 x 5 = 3 x 6
A , B , C có bội chung nhỏ nhất là 6
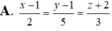
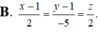
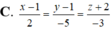
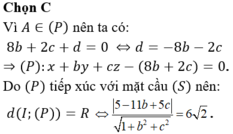
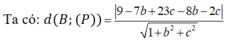
\(M_Z=23.M_{H_2}=23.2=46\left(\dfrac{g}{mol}\right)\\ \Rightarrow Z:C_2H_5OH\\ \Rightarrow Y:CH_3COONa\\ \Rightarrow X:CH_3COOC_2H_5\\ PTHH:CH_3COOC_2H_5+NaOH\underrightarrow{to}CH_3COONa+C_2H_5OH\)
=> X : etyl axetat
=> CHỌN A
A