Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
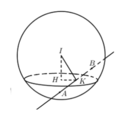
Phương pháp: AB lớn nhất
Cách giải: Mặt cầu (S) có tâm I(0;-2;0) và bán kính R = 5
Ta có
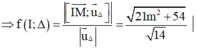
Để AB lớn nhất
Đáp án C
Ta có: M ∈ ( P )
O M 2 = 6 < R 2 = 9 ⇒ M nằm trong mặt cầu ⇒ (P) cắt mặt cầu thành 1 hình tròn (C)
Gọi H là tâm hình tròn (C)
Để AB nhỏ nhất thì A B ⊥ H M
Vì 
O là tâm mặt cầu và O (0; 0; 0)
Phương trình OH: x = t y = t z = t
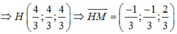
là một vecto chỉ phương của AB
Chọn 
là vecto chỉ phương của AB
Thì 
Chọn C
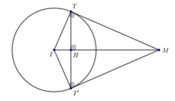
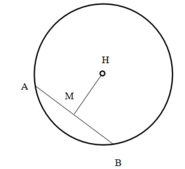
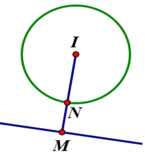
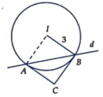
Mặt cầu (S) có tâm I(1;2;3), bán kính R =2. Mặt phẳng (ITT') cắt d tại điểm M (như hình vẽ trên). Gọi H là giao điểm của TT' và MI.
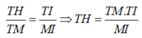
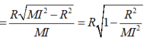
Do TT' = 2TH nên
Nhận xét rằng với
nên khi thay đổi ta luôn có
cố định. Vì thế
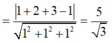
Từ đó ta có:
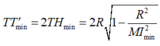
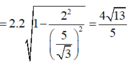
Ta kiểm tra điều kiện đủ của bài toán, tức là chứng minh rằng hình chiếu vuông góc của I lên (P) thuộc vào đường thẳng d.
Gọi d' là đường thẳng qua I và vuông góc với ta có:
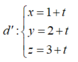
Gọi M là hình chiếu vuông góc của I lên (P) ta có:
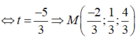
Xét hệ
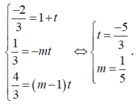
Vậy với m = 1 5 thì độ dài của TT' nhỏ nhất.
6.
Mặt phẳng Oxz có pt: \(y=0\)
Khoảng cách từ I đến Oxz: \(d\left(I;Oxz\right)=\left|y_I\right|=2\)
\(\Rightarrow R=2\)
Phương trình mặt cầu:
\(\left(x-1\right)^2+\left(y-2\right)^2+\left(z-3\right)^2=4\)
7.
Mặt phẳng (Q) nhận \(\left(1;-2;3\right)\) là 1 vtpt nên cũng nhận các vecto có dạng \(\left(k;-2k;3k\right)\) là vtpt
Bạn có ghi nhầm đề bài ko nhỉ? Thế này thì cả C và D đều ko phải vecto pháp tuyến của (Q)
4.
Đường thẳng d nhận \(\left(1;-2;2\right)\) là 1 vtcp
Gọi (P) là mặt phẳng qua M và vuông góc d \(\Rightarrow\) (P) nhận \(\left(1;-2;2\right)\) là 1 vtpt
Phương trình (P): \(1\left(x-2\right)-2\left(y-3\right)+2\left(z+1\right)=0\)
\(\Leftrightarrow x-2y+2z+6=0\)
Pt d dạng tham số: \(\left\{{}\begin{matrix}x=4+t\\y=1-2t\\z=5+2t\end{matrix}\right.\)
Tọa độ hình chiếu M' của M lên d là giao của d và (P) nên thỏa mãn:
\(4+t-2\left(1-2t\right)+2\left(5+2t\right)+6=0\) \(\Rightarrow t=-2\)
\(\Rightarrow M'\left(2;5;1\right)\)
5.
(P) nhận \(\left(2;3;1\right)\) là 1 vtpt
Gọi d là đường thẳng qua I và vuông góc (P)
\(\Rightarrow\) d nhận \(\left(2;3;1\right)\) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=1+2t\\y=-2+3t\\z=1+t\end{matrix}\right.\)
H là giao điểm của d và (P) nên tọa độ thỏa mãn:
\(2\left(1+2t\right)+3\left(-2+3t\right)+1+t-11=0\) \(\Rightarrow t=1\)
\(\Rightarrow H\left(3;1;2\right)\)
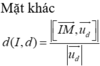
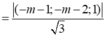
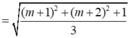
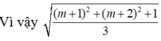
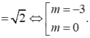
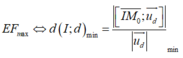
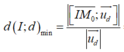
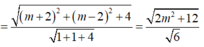
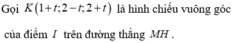
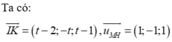
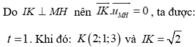
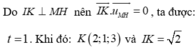
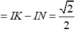
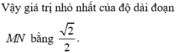
Mặt cầu (S) có tâm I (1;0;-2) và bán kính R=2.
Đường thẳng d đi qua điểm N (2; 0; m-1) và có véc tơ chỉ phương
Điều kiện để d cắt (S) tại hai điểm phân biệt là d (I; (d))<R
Khi đó, tiếp diện của (S) tại A và B vuông góc với IA và IB nên góc giữa chúng là góc (IA;IB).
Vậy T= {-3;0}. Tổng các phần tử của tập hợp T bằng -3.