Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc của xe máy là x (km/h; x > 0)
Vận tốc của ô tô là x + 24 (km/h)
Thời gian xe máy đi hết quãng đường là: 120/x (h)
Thời gian ô tô đi hết quãng đường là: 120/(x+4) (h)
Đổi 30 phút = 1/2 (h), 20 phút = 1/3 (h)
Theo đề bài ta có phương trình:
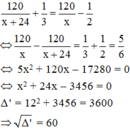
Phương trình có hai nghiệm x 1 = − 12 – 60 = −72 (loại) và x 2 = −12 + 60 = 48 (tmđk)
Vậy vận tốc xe máy là 48 km/h và vận tốc ô tô là 48 + 24 = 72 km/h
Đáp án: D

Lời giải:
Gọi vận tốc lúc về là $a$ (km/h) thì vận tốc lúc đi là $a+10$ (km/h)
Thời gian cả đi cả về là: $6h44'-2h20'=4h24'=4,4$ (giờ)
Thời gian đi: $AB:(a+10)=\frac{120}{a+10}$ (h)
Thời gian về: $AB:a=\frac{120}{a}$ (h)
Tổng thời gian đi và về: $\frac{120}{a+10}+\frac{120}{a}=4,4$
Giải pt trên thu được $a=50$ (km/h)
Vạn tốc ô tô lúc đi: $a+10=60$ (km/h)

Gọi \(x\left(km/h\right)\) là vận tốc lúc đi và lúc về \(\left(x>0\right)\)
\(x+10\) là vận tốc lúc về \(\left(km/h\right)\)
Đổi \(2h12p=2,2h\)
Theo đề, ta có pt :
\(\dfrac{60}{x}+\dfrac{60}{x+10}=2,2\)
\(\Leftrightarrow60\left(x+10\right)+60x-2,2x\left(x+10\right)=0\)
\(\Leftrightarrow60x+600+60x-2,2x^2-22x=0\)
\(\Leftrightarrow-2,2x^2+98x+600=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=50\left(tmdk\right)\\x=-\dfrac{60}{11}\left(ktmdk\right)\end{matrix}\right.\)
Vậy vận tốc lúc đi là \(50km/h\)
lúc về là : \(50+10=60\left(km/h\right)\)

Gọi vận tốc trung bình của ô tô là x
Sau 3h xe máy đi được 3(x-10)(km)
theo đề, ta có:
(3x-30+30)/(x-10)=30/x
=>3x/(x-10)=30/x
=>3x^2=30x-300
=>x^2-10x+100=0
=>Ko có vận tốc của ô tô thỏa mãn

Gọi x (km) là quãng đường AB
Thời gian ô tô đi hết QĐ AB là \(\frac{x}{40}\) (giờ)
Thời gian taxi đi hết AB là \(\frac{x}{60}\) (giờ)
2 giờ30 phút = 2,5 giờ
Taxi xuất phát sau ô tô 2,5 giờ và 2 xe đến cùng 1 lúc nên ta có phương trinh:
\(\frac{x}{40}\) - \(\frac{x}{60}\) = 2,5
<=> 3x - 2x = 300
=> x = 300
Vậy qđ AB dài 300 km
Gọi quãng đường AB là x (Đk x> 0 )
THời gian đi từ A - B của xe ô tô tải là x/40 ( giờ)
Thời gian đi từ A - B của xe taxi là : x/60
Đổi 2 h30p = 2,5 h
THeo bài ra ta có pt
x / 40 - x/60 = 2,5
6x - 4x = 2,5.240
2x = 600
x = 300
VẬy quãng đg AB là 300km

Gọi vận tốc người 1 là x
Vận tốc người 2 là x+10
Theo đề, ta có: \(\dfrac{150}{x}-\dfrac{150}{x+10}=\dfrac{1}{2}\)
=>\(\dfrac{150x+1500-150x}{x^2+10x}=\dfrac{1}{2}\)
=>x^2+10x-3000=0
=>(x+60)(x-50)=0
=>x=50
=>vận tốc xe 2 là 60km/h

Gọi vận tốc ô tô là: x ( km/h ) ( x > 24 )
=) vận tốc xe máy là: x - 24 ( km/h )
Thời gian để ô tô đi hết quãng đường AB là: \(\frac{120}{x}\)( giờ )
Thời gian đẻ xe máy đi hết quãng đường AB là: \(\frac{120}{x-24}\)( giờ )
VÌ ô tô đến B được \(\frac{4}{3}\)giờ thì xe máy mới đén A cũng như ô tô đi trươc xe máy \(\frac{1}{2}\)giờ nên ta có phương trình:
\(\frac{120}{x-24}-\frac{4}{3}=\frac{120}{x}-\frac{1}{2}\)
\(\frac{120}{x-24}-\frac{120}{x}=\frac{5}{6}\)
\(\frac{720x}{6x.\left(x-24\right)}-\frac{720.\left(x-24\right)}{6x.\left(x-24\right)}=\frac{5x.\left(x-24\right)}{6x.\left(x-24\right)}\)
\(720x-720+17280=5x^2-120x\)
\(5x^2-120x-17280=0\)
\(x^2-24x-3456=0\)
\(\left(x-72\right).\left(x+48\right)=0\)
\(\orbr{\begin{cases}x=72\\x=-48\left(lo\text{ại}\right)\end{cases}}\)
Vận tốc ô tô là: 72 km/h
Vận tốc xe máy là: 48 km/h
Gọi vận tốc xe máy là x (km/h) (x>0)
thì vận tốc ô tô là: x + 24 (km/h)
Thời gian xe máy đi quãng đường AB là: \(\frac{120}{x}\)(h)
Thời gian ô tô đi quãng đường AB là:\(\frac{120}{x+24}\)(h)
Thời gian xe máy đi nhiều hơn ô tô: 1h20' - (7h30' - 7h) = 50' = \(\frac{5}{6}\) (h)
Ta có phương trình: \(\frac{120}{x}-\frac{120}{x+24}=\frac{5}{6}\)
<=> 6.[120(x+24) - 120x] = 5x(x+24)
<=> 720(x+24) - 720x = 5x^2 + 120x
<=> 5x^2 + 120x - 17280 = 0
<=> x = 48 (TMĐK) hoặc x = -72 (không TMĐK)
Vậy vận tốc xe máy là 48 km/h
vận tốc ô tô là: 48+24=72 (km/h)
Thời gian để ô tô đi hết quãng đường AB là :
\(99:45=2,2\)( giờ )
\(=\)2 giờ 12 phút
Vậy ô tô đã đi từ A lúc :
10 giờ 12 phút - 2 giờ 12 phút = 8 ( giờ )
Đáp số : 8 giờ
Thời gian ô tô đi trên đường là :
99 : 45 = 2,2 (giờ) = 2 giờ 12 phút
Ô tô đã đi từ tỉnh A lúc :
10 giờ 12 phút - 2 giờ 12 phút = 8 giờ
Đáp số : 8 giờ