Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi chiều rộng của mảnh đất hình chữ nhật là x (m) (0 < x < 13)
Chiều dài mảnh đất hình chữ nhật lớn hơn chiều rộng 7m nên chiều dài của mảnh đất hình chữ nhật là x + 7 (m)
Biết độ dài đường chéo là 13m nên theo định lý Pitago ta có phương trình:
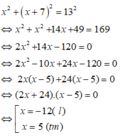
Vậy chiều rộng mảnh đất hình chữ nhật là 5m và chiều dài mảnh đất đó là 12m.
Chọn đáp án C

Ta có \(225=15.15\) \(\Rightarrow\)Độ dài 1 cạnh của mảnh đất là 15m
Chu vi mảnh đất hình vuông là
\(15.4=60\left(m\right)\)
Đáp số \(60m\)

Gọi chiều dài, chiều rộng hcn là \(a,b>0\left(m\right)\)
Ta có chu vi hình chữ nhật là 28m nên
\(2\left(a+b\right)=28\Leftrightarrow a+b=14\\ \Leftrightarrow b=14-a\)
Vì đường chéo hình chữ nhật là 10 nên
\(a^2+b^2=100\left(Pytago\right)\)
\(\Leftrightarrow a^2+\left(14-a\right)^2=100\\ \Leftrightarrow2a^2-28a+96=0\\ \Leftrightarrow a^2-14a+48=0\\ \Leftrightarrow\left(a^2-6a\right)-\left(8a-48\right)=0\\ \Leftrightarrow\left(a-6\right)\left(a-8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=6\Rightarrow b=8\\a=8\Rightarrow b=6\end{matrix}\right.\)
Vậy độ dài 2 cạnh mảnh đất là 6m và 8m

Ta có Cv hcn ABCD=28(m)
=>AB+BC=14(m) (1)
=>(AB+BC)\(^2\) =14\(^2\) (m)
=>AB\(^2\) +BC\(^2\) +2AB.BC=196(m)
Do ΔABC là Δ vuông
=>AD\(^2\) +2AB.BC=196(m)
=>2AB.BC=96
=>AB.BC=48
=>AB=\(\dfrac{48}{BC}\)
Thay vào (1), ta có :
BC+\(\dfrac{48}{BC}\) =14
giải ra đc BC=8
AB=6


S=1/2*a*b