Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chiều dài, chiều rộng lần lượt là a,b
Theo đề, ta có:
a+b=160 và a=3b
=>a=120 và b=40

Gọi chiều dài, chiều rộng hcn là \(a,b>0\left(m\right)\)
Ta có chu vi hình chữ nhật là 28m nên
\(2\left(a+b\right)=28\Leftrightarrow a+b=14\\ \Leftrightarrow b=14-a\)
Vì đường chéo hình chữ nhật là 10 nên
\(a^2+b^2=100\left(Pytago\right)\)
\(\Leftrightarrow a^2+\left(14-a\right)^2=100\\ \Leftrightarrow2a^2-28a+96=0\\ \Leftrightarrow a^2-14a+48=0\\ \Leftrightarrow\left(a^2-6a\right)-\left(8a-48\right)=0\\ \Leftrightarrow\left(a-6\right)\left(a-8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=6\Rightarrow b=8\\a=8\Rightarrow b=6\end{matrix}\right.\)
Vậy độ dài 2 cạnh mảnh đất là 6m và 8m

Gọi chiều dài mảnh đất là x (m)(x > 6)
Chiều rộng mảnh đất là x – 6 (m)
Chu vi mảnh đất là 2(x + x – 6) = 4x – 12 (m)
Theo định lí Py-ta-go ta có bình phương đường chéo của mảnh đất là x 2 + ( x – 6 ) 2
Vì bình phương đường chéo gấp 5 lần chu vi nên ta có phương trình:
x 2 + ( x – 6 ) 2 = 5 ( 4 x – 12 ) ⇔ x 2 + x 2 – 12 x + 36 = 20 x – 60
⇔ 2 x 2 – 32 x + 96 = 0 ⇔ x 2 – 16 x + 48 = 0
⇔ (x – 12)(x – 4) = 0 ⇔ x = 12 (tmđk) hoặc x = 4 (không tmđk x > 6)
Vậy chiều dài của mảnh đất là 12m, chiều rộng của mảnh đất là 6m

2 chiều là x, y
=>
x + y = 14
x^2 + y^2 = 100
<=>
x = 14 - y
(14-y)2+y2 = 100
<=>
x = 14 - y
196 - 28y + y2 + y2 = 100
<=>
x = 14 - y
2y2 - 28y + 96 = 0
<=>
x = 14 - y
y = 6 hoặc y = 8
<=>
x = 8, y = 6
hoặc x = 6, y = 8
=> chiều dài: 8m, chiều rộng: 6m
gọi chiều dài. chiều rộng hcn lần lượt là a,b(a>b>0)
ta có(a+b).2=28
<=> a+b=14
=> a=14-b
lại có a^2+b^2=10^2
<=>(14-b)^2+b^2=100
<=>196-28b+2b^2=100
<=>[b=8=> a=6(loại)
[b=6=>a=8
Vậy chiều dài: 8 m
chiều rộng: 6 m

Nửa chu vi mảnh vườn là: \(140:2=70\left(m\right)\)
Gọi chiều dài mảnh vườn là x (m) với x>0
Chiều rộng mảnh vườn là: \(\dfrac{2x}{5}\) (m)
Do nửa chu vi mảnh vườn là 70m nên ta có pt:
\(x+\dfrac{2x}{5}=70\)
\(\Leftrightarrow\dfrac{7x}{5}=70\)
\(\Leftrightarrow x=50\left(m\right)\)
Vậy mảnh vườn có chiều dài 50m, chiều rộng 20m

Gọi chiều rộng của mảnh đất hình chữ nhật là x (m) (0 < x < 13)
Chiều dài mảnh đất hình chữ nhật lớn hơn chiều rộng 7m nên chiều dài của mảnh đất hình chữ nhật là x + 7 (m)
Biết độ dài đường chéo là 13m nên theo định lý Pitago ta có phương trình:
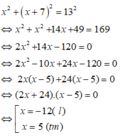
Vậy chiều rộng mảnh đất hình chữ nhật là 5m và chiều dài mảnh đất đó là 12m.
Chọn đáp án C


Ta có Cv hcn ABCD=28(m)
=>AB+BC=14(m) (1)
=>(AB+BC)\(^2\) =14\(^2\) (m)
=>AB\(^2\) +BC\(^2\) +2AB.BC=196(m)
Do ΔABC là Δ vuông
=>AD\(^2\) +2AB.BC=196(m)
=>2AB.BC=96
=>AB.BC=48
=>AB=\(\dfrac{48}{BC}\)
Thay vào (1), ta có :
BC+\(\dfrac{48}{BC}\) =14
giải ra đc BC=8
AB=6