Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D
Số phần tử không gian mẫu: 
Gọi A là biến cố: Có 3 người cùng đến quầy thứ nhất .
Số kết quả thuận lợi của biến cố A là: 
Xác suất của biến cố A: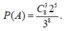 
Mỗi hành khách có 3 lựa chọn \(\Rightarrow n\left(\Omega\right)=3^{12}\)
Chọn 4 người lên toa 1: \(C_{12}^4\) cách
Còn lại 8 người lên 2 toa còn lại, có \(2^8\) cách
Xác suất: \(\dfrac{C_{12}^4.2^8}{3^{12}}=...\)
Đáp án C.
Gọi 
là tập tất cả các dãy số 
trong đó 
là số toa mà hành khách thứ i lên 
+ 
là tập các cách lên tàu sao cho có 2 toa có 3 người và mỗi toa còn lại 1 người
+ 
là tập các cách lên tàu sao cho có 2 toa có 2 người và 1 toa có 1 người
là biến cố “Mỗi toa đều có hành khách lên tàu”
Chọn B
Số cách xếp ngẫu nhiên là 5! cách.
Ta tìm số cách xếp thoả mãn:
+ Chọn 2 vị trí cạnh nhau (3,4) và (4,5) có 2 cách.
+ Xếp A và B vào 2 vị trí cạnh nhau vừa chọn có 2! cách.
+ Xếp 3 người còn lại có 3! cách.
Số cách xếp là 2.2!3!. Xác suất cần tính bằng 
.
Đáp án B
Số cách để 4 vị khách lên tàu là: 
Số cách để chọn 3 vị khách lên một toa tàu là 
Số cách chọn 1 trong 3 toa là 
Vị khách còn lại có 2 cách chọn lên toa tàu
Vậy số cách để 1 trong 3 toa tàu chứa 3 trong 4 vị khách là: 3.4.2=24
Chọn A
Số phần tử không gian mẫu: 
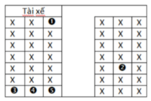
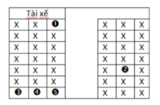
Gọi A là biến cố: Mỗi toa có ít nhất một khách lên tàu .
Có hai trường hợp:
TH1: Một toa có 3 khách 2 toa còn lại mỗi toa có 1 khách.
Trường hợp này có: 
(cách).
TH 2: Một toa có 1 khách 2 toa còn lại mỗi toa có 2 khách.
Trường hợp này có:
(cách).
Số kết quả thuận lợi của biến cố A là: n(A) = 150(cách).
Xác suất của biến cố A : 
Đáp án A
Số phần tử của không gian mẫu
*Gọi A là biến cố cần tính xác suất;
theo giả thiết bài toán chỉ có một cửa hàng mà có số khách vào là 3, 4 hoặc 5.
TH1: Một cửa hàng có 3 vị khách vào
+) Chọn 1 trong 5 cửa hàng có C 5 1 cách.
+) Chọn 3 trong 5 vị khách có C 5 3 cách.
+) 3 khách vừa chọn sẽ vào cửa hàng vừa chọn ở trên có 1 cách.
+) 2 khách còn lại mỗi khách có 4 lựa chọn nên có 4 2 cách.
Vậy trường hợp này có C 5 1 . C 5 3 . 4 2 cách.
TH2: Một cửa hàng có 4 vị khách vào, có tất cả C 5 1 . C 5 4 . 4 cách.
TH3: Một cửa hàng có 5 vị khách vào, có tất cả C 5 1 . C 5 5 cách.
Xác suất cần tính