Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C
Số phần tử của không gian mẫu: .
Gọi biến cố : “Xếp 10 học sinh vào 10 ghế sao cho mỗi học sinh nam đều ngồi đối diện một học sinh nữ”.
Giả sử đánh vị trí ngồi như bảng sau:
Cách 1: Xếp vị trí A 1 có 10 cách. Mỗi cách xếp vị trí A 1 sẽ có 5 cách xếp vị trí B 1 .
Mỗi cách xếp vị trí A 1 , B 1 có 8 cách xếp vị trí , tương ứng sẽ có 4 cách xếp vị trí B 2 .
Cứ làm như vậy thì số cách xếp thỏa mãn biến cố là:
Cách 2: Đánh số cặp ghế đối diện nhau là C1, C2, C3, C4, C5
Xếp bạn nam vào 5 cặp ghế có 5! cách.
Ở mỗi cặp ghế, ta có 2 cách xếp một cặp nam, nữ ngồi đối diện.
Số phần tử của A là: 
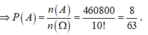
Ít nhất 1 xe tốt, vậy nhiều nhất là 4 xe tốt :)
TH1: 1 xe tốt \(C^1_{10}.C^3_5\) (cách)
TH2: 2 xe tốt \(C^2_{10}.C^2_5\) (cách)
TH3: 3 xe tốt \(C^3_{10}.C^1_5\) (cách)
TH4: 4 xe tốt \(C^4_{10}.C^0_5\) (cách)
\(\Rightarrow n\left(A\right)=C^1_{10}.C^3_5+C^2_{10}.C^2_5+C^3_{10}.C^1_5+C^4_{10}.C^0_5=...\)
Không gian mẫu: \(n\left(\Omega\right)=C^4_{15}\)
\(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=...\)
Chọn D
Cách 1. Xếp ngẫu nhiên 10 học sinh vào hai dãy ghế có cách.
Đánh số ghế lần lượt từ 1 đến 10.
Xếp học sinh thỏa mãn bài toán xảy ra hai khả năng sau:
Khả năng 1: Nam ngồi vị trí lẻ, nữ ngồi vị trí chẵn có 5!.5! cách.
Khả năng 2: Nam ngồi vị trí chẵn, nữ ngồi vị trí lẻ có 5!.5! cách.
Vậy có tất cả 2. ( 5 ! ) 2 cách.
Xác suất cần tìm bằng 
Cách 2: Xếp ngẫu nhiên 10 học sinh vào hai dãy ghế, có 10! cách xếp.
Ta chia hai dãy ghế thành 5 cặp ghế đối diện:
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 1 có 
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 2 có 
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 3 có 
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 4 có 
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 5 có 1 cách.
Vậy có tất cả 
cách xếp thỏa mãn.
Xác suất cần tìm bằng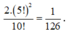 
Chọn B
Số cách xếp ngẫu nhiên là 5! cách.
Ta tìm số cách xếp thoả mãn:
+ Chọn 2 vị trí cạnh nhau (3,4) và (4,5) có 2 cách.
+ Xếp A và B vào 2 vị trí cạnh nhau vừa chọn có 2! cách.
+ Xếp 3 người còn lại có 3! cách.
Số cách xếp là 2.2!3!. Xác suất cần tính bằng