K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 7 2021
Xét ΔAMB có
MD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AM}{MB}\)(1)
Xét ΔAMC có
ME là đường phân giác ứng với cạnh AC
nên \(\dfrac{AE}{EC}=\dfrac{AM}{MC}\)(2)
Ta có: M là trung điểm của BC(gt)
nên MB=MC(3)
Từ (1), (2) và (3) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
hay DE//BC(đpcm)
PL
1
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 12 2021
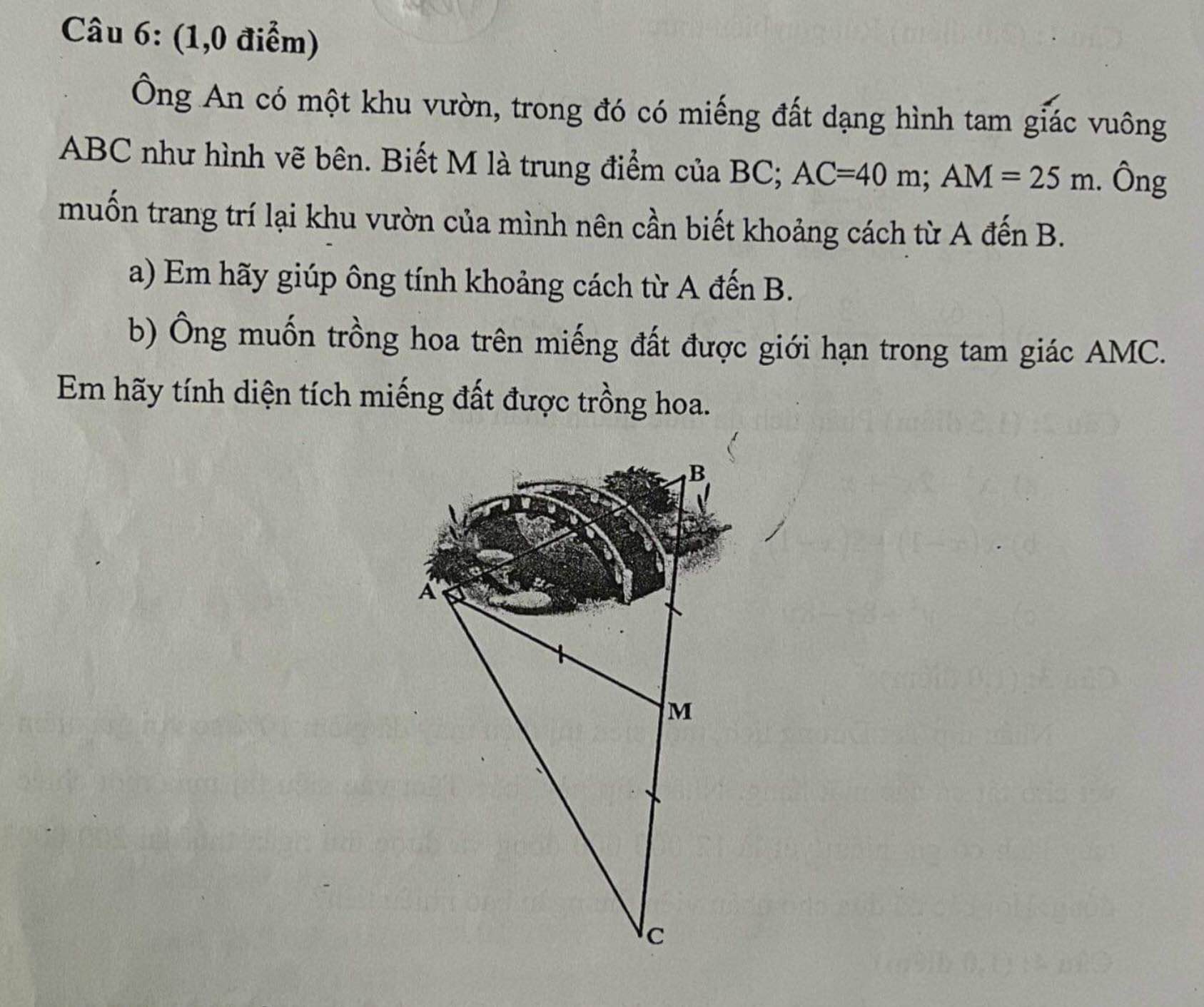
Tam giác ABC vuông tại A có AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC=2AM=50\left(m\right)\)
a. Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2-AC^2}=30\left(m\right)\)
b. Kẻ \(MH\perp AC\Rightarrow MH||AB\) (cùng vuông góc AC)
Mà M là trung điểm BC \(\Rightarrow MH\) là đường trung bình tam giác ABC
\(\Rightarrow MH=\dfrac{1}{2}AB=15\left(m\right)\)
\(\Rightarrow S_{AMC}=\dfrac{1}{2}MH.AC=\dfrac{1}{2}.15.40=300\left(m^2\right)\)
15 tháng 12 2022
a: =>(x+3)(5-2x)=0
=>x=-3 hoặc x=5/2
b: =>(x-3)(5x+20)=0
=>x=-4 hoặc x=3
c: =>(x-2)(5x+1)=0
=>x=2 hoặc x=-1/5
d: =>(x-1)(x+2)=0
=>x=-2 hoặc x=1
e: =>(2x+1)^2=0
=>2x+1=0
=>x=-1/2
f:=>(3x-5)(3x+3)=0
=>x=-1 hoặc x=5/3
JN
1
8 tháng 4 2023
- Bài này phải có điều kiện \(x>0\) thì mới làm được nhé bạn.
NH
9 tháng 4 2023
À mình cảm ơn bạn nhá mình cũng vừa mới xem lại đề cô gửi thì mình thấy có điều kiện x>0 thật mình cảm ơn bạn nhiều nhá
TT
26 tháng 3 2021
Bài 1:
a.Xét tam giác PNM và tam giác PQR ,ta có :
A^=Q^(= 90 độ )
P1^= P2^(đối đỉnh )
=>tam giác PNMđồng dạng tam giác PQR
b.ta có: MN//PR
=>NPtrên PQ=MN trên QR
=>x=3 nhân 6 trên 2
=>x=9
