K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PL
Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều
0
30 tháng 12 2021
a: Xét tứ giác ANME có
\(\widehat{ANM}=\widehat{AEM}=\widehat{EAN}=90^0\)
Do đó: ANME là hình chữ nhật
LN
1
NK
0
TN
0
1 tháng 11 2021
a, Vì ABCD là hbh nên AB//CD
Do đó \(\widehat{A}+\widehat{D}=180^0\Rightarrow3\widehat{D}=180^0\Rightarrow\widehat{D}=60^0\Rightarrow\widehat{A}=120^0\)
Mà ABCD là hbh nên \(\left\{{}\begin{matrix}\widehat{A}=\widehat{C}=120^0\\\widehat{D}=\widehat{B}=60^0\end{matrix}\right.\)
b, Vì CE=CB nên tam giác CEB cân tại C
Do đó \(\widehat{B}=\widehat{CEB}\)
\(\Rightarrow\widehat{D}=\widehat{CEB}\left(1\right)\)
Mà ABCD là hbh nên AB//CD hay AE//CD
Do đó AECD là hình thang
Kết hợp (1) ta được AECD là hthang cân
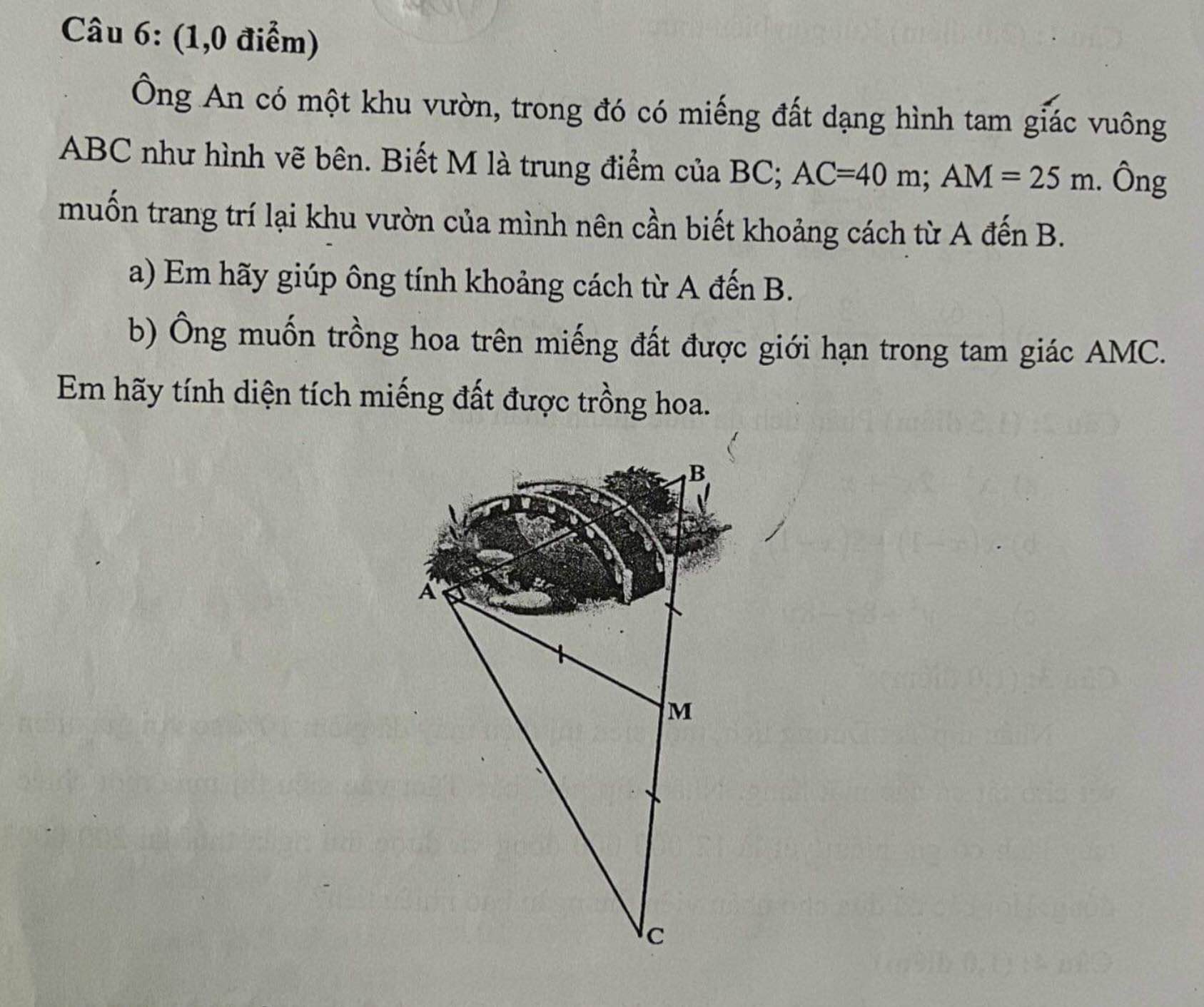
Tam giác ABC vuông tại A có AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC=2AM=50\left(m\right)\)
a. Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2-AC^2}=30\left(m\right)\)
b. Kẻ \(MH\perp AC\Rightarrow MH||AB\) (cùng vuông góc AC)
Mà M là trung điểm BC \(\Rightarrow MH\) là đường trung bình tam giác ABC
\(\Rightarrow MH=\dfrac{1}{2}AB=15\left(m\right)\)
\(\Rightarrow S_{AMC}=\dfrac{1}{2}MH.AC=\dfrac{1}{2}.15.40=300\left(m^2\right)\)
Cảm ơn nhiều ạ ;-;