NL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 7 2021
a. TXĐ: \(D=R\)
Với mọi \(x\in D\Rightarrow x\pm2\pi\in D\)
Đồng thời:
\(y\left(x+2\pi\right)=sin\left(x+2\pi\right)+cos\left(2x+4\pi\right)=sinx+cos2x=y\left(x\right)\)
\(\Rightarrow\) Hàm là hàm tuần hoàn với chu kì \(T=2\pi\)
b. TXĐ: \(D=R\)
Với mọi \(x\in D\Rightarrow x\pm\dfrac{2\pi}{3}\in D\)
\(y\left(x+\dfrac{2\pi}{3}\right)=sin\left(3x+2\pi\right)=sin3x=y\left(x\right)\)
\(\Rightarrow\) Hàm là hàm tuần hoàn với chu kì \(T=\dfrac{2\pi}{3}\)
PT
1
CM
14 tháng 2 2017
Ta có y = 2cos2x – 1 = cos2x, do đó hàm số tuần hoàn với chu kì T = 2π/2 = π.
Vậy đáp án là A.
19 tháng 8 2021
Ta có \(y\left(x+\pi\right)=cos\left[sin\left(x+\pi\right)\right]=cos\left(-sinx\right)=cos\left(sinx\right)\)
nên \(y\left(x+2\pi\right)=y\left(x\right)\)
Tuần hoàn với chu kì π
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 8 2021
TXĐ: \(D=R\)
Với mọi \(x\in R\) thì \(x+\pi\in R\)
Ta có:
\(f\left(x\right)=cos\left(sinx\right)\)
\(f\left(x+\pi\right)=cos\left(sin\left(x+\pi\right)\right)=cos\left(-sinx\right)=cos\left(sinx\right)=f\left(x\right)\)
\(\Rightarrow\) Hàm tuần hoàn với chu kì \(T=\pi\)
Giả sử tồn tại \(0< T_0< \pi\) sao cho \(f\left(x+T_0\right)=f\left(x\right)\); \(\forall x\)
\(\Leftrightarrow cos\left[sin\left(x+T_0\right)\right]=cos\left(sinx\right)\)
Thay \(x=0\Rightarrow cos\left(sinT_0\right)=cos0=1\) (1)
Do \(0< T_0< \pi\Rightarrow0< sinT_0< 1\Rightarrow cos\left(sinT_0\right)< 1\)
\(\Rightarrow\) (1) sai hay điều giả sử là sai
Vậy \(T=\pi\) là chu kì của hàm đã cho
CM
25 tháng 12 2019
Hàm số y 1 = sin π 2 − x có chu kì T 1 = 2 π − 1 = 2 π
Hàm số y 2 = cot x 3 có chu kì T 2 = π 1 3 = 3 π
Suy ra hàm số đã cho y = y 1 + y 2 có chu kì T = B C N N 2 , 3 π = 6 π .
Vậy đáp án là D.
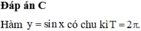
\(\left|sin\left(x+\pi\right)\right|=\left|-sinx\right|=\left|sinx\right|\)
\(\Rightarrow\) Hàm \(y=\left|sinx\right|\) tuần hoàn với chu kì \(T=\pi\)