K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 12 2021
Áp dụng tc dtsbn:
\(\dfrac{2y+z-x}{x}=\dfrac{2z-y+x}{y}=\dfrac{2x+y-z}{z}=\dfrac{2x+2y+2z}{x+y+z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\\ \Rightarrow\left\{{}\begin{matrix}2y+z-x=2x\\2z-y+x=2y\\2x+y-z=2z\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2y+z=3x\\2z+x=3y\\2x+y=3z\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3x-2y=z\\3y-2z=x\\3z-2x=y\end{matrix}\right.;\left\{{}\begin{matrix}3x-z=2y\\3y-x=2z\\3z-y=2z\end{matrix}\right.\\ \Rightarrow P=\dfrac{xyz}{2x\cdot2y\cdot2z}=\dfrac{1}{8}\)
Chọn D
CC
2
22 tháng 10 2021
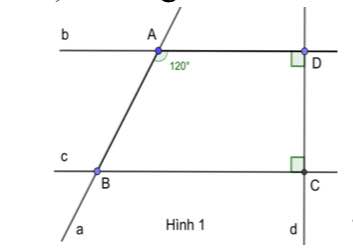
a, Vì b và c cùng vuông góc với d nên b//c
b, Vì b//c nên \(\widehat{A}=\widehat{ABc}=120^0\left(so.le.trong\right);\widehat{A}=\widehat{BCa}=120^0\left(đồng.vị\right)\)
Ta có \(\widehat{ABc}+\widehat{ABC}=180^0\left(kề.bù\right)\Rightarrow\widehat{ABC}=180^0-120^0=60^0\)
Ta có \(\widehat{aBc}=\widehat{ABC}=60^0\left(đối.đỉnh\right)\)
22 tháng 10 2021
vì b//c
=> \(\widehat{DAB}+\widehat{ABC}=180\) ( 2 góc trong cùng phía bù nhau )
=> \(120+\widehat{ABC}=180=>\widehat{ABC}=60\)
=> \(\widehat{ABC}=\widehat{cBa}=60\) ( đối đỉnh)
\(\widehat{ABC}+\widehat{ABc}=180\) ( 2 góc kề bù)
=> \(60+\widehat{ABc}=180=>\widehat{ABc}=120\)
\(\widehat{ABc}=\widehat{aBC}=120\) đối đỉnh
VT
1
TT
18 tháng 12 2020
Có
\(\left|x-2\right|+\left|x-4\right|=\left|x-2\right|+\left|4-x\right|\ge\left|x-2+4-x\right|=2\)
\(\left|x-3\right|\ge0\)
=> \(\left|x-2\right|+\left|x-4\right|+\left|x-3\right|\ge2\)
Dấu "=" xảy ra
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\x-2>0\\4-x>0\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}x=3\\x-2< 0\\4-x< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=3\\x>2\\x< 4\end{matrix}\right.\\\left\{{}\begin{matrix}x=3\\x< 2\\x>4\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x=3\)
AV
3 tháng 5 2018
Ta có: f(x)=x2+2
Cho f(x)=0 ⇒ x2+2=0 ⇒x2= -2 (vô lý với mọi x )
Vậy f(x)= x2-x-x+2 vô nghiệm (đpcm)
AV
9 tháng 5 2018
Xin lỗi sai đề 
.Đề đúng nè
Ta có: f(x)=x2-2x+2
Cho : f(x)=x2-2x+2=0 => f(x)=(x2-2x+1)+1=0
=> f(x)=(x-1)2+1=0 (bất đẳng thức lớp 8 lận đó)
=> f(x)=(x-1)2= -1 (vô lý)
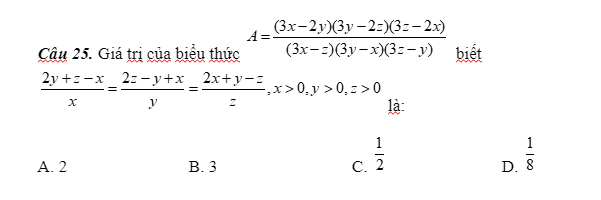
\(1,\Rightarrow3:\dfrac{9}{4}=\dfrac{3}{4}:x\\ \Rightarrow\dfrac{4}{3}=\dfrac{3}{4}:x\\ \Rightarrow x=\dfrac{3}{4}:\dfrac{4}{3}=\dfrac{9}{16}\\ 2,\)
Nửa chu vi là \(50:2=25\left(cm\right)\)
Gọi cd là a, cr là b (cm)(a,b>0)
Ta có \(a:b=3:2\Rightarrow\dfrac{a}{3}=\dfrac{b}{2}\) và \(a+b=25\left(cm\right)\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{3}=\dfrac{b}{2}=\dfrac{a+b}{3+2}=\dfrac{25}{5}=5\\ \Rightarrow\left\{{}\begin{matrix}a=15\\b=10\end{matrix}\right.\)
Vậy ...
B2:chiều dài là 15
Chiều rộng là 10