Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Với PT bậc 2, nếu \(z_1\) là một nghiệm phức thì nghiệm \(z_2\) còn lại chính là số phức liên hợp của \(z_1\). Khi đó áp dụng hệ thức Viete:
\(\left[{}\begin{matrix}W=\dfrac{z_1+2016^{2017}}{z_2+1}=\dfrac{z_1+z_1z_2}{z_2+1}=z_1\\W=\dfrac{z_2+2016^{2017}}{z_1+1}=\dfrac{z_2+z_1z_2}{z_1+1}=z_2\end{matrix}\right.\)
Vì \(z_1,z_2\) là hai số liên hợp của nhau nên có phần thực như nhau. Do đó phần thực của \(W\) chính bằng \(\frac{z_1+z_2}{2}=1\) (theo hệ thức Viete)
Đáp án B

Chọn C.
Đặt t = f ( x ) → d t = f ' x d x . Đổi cận: x = 2016 → t = f ( 2016 ) = a x = 2017 → t = f ( 2017 ) = b
Khi đó
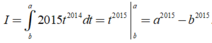

|
1 |
B |
6 |
B |
11 |
C |
16 |
A |
21 |
D |
|
2 |
C |
7 |
A |
12 |
A |
17 |
B |
22 |
D |
|
3 |
A |
8 |
B |
13 |
B |
18 |
C |
23 |
C |
|
4 |
B |
9 |
B |
14 |
A |
19 |
A |
24 |
A |
|
5 |
D |
10 |
C |
15 |
D |
20 |
D |
25 |
C |

ĐKXĐ: \(x\ge-2\)
Hàm \(f\left(x\right)=\sqrt{2x+4}+\sqrt[3]{3x+1}\) có \(f'\left(x\right)=\frac{1}{\sqrt{2x+4}}+\frac{1}{\sqrt[3]{\left(3x+1\right)^2}}>0\) với mọi x thuộc khoảng xác định nên hàm đồng biến
\(\Rightarrow\) Nghiệm của BPT là \([-2;a)\)
Trong đó a là nghiệm thực của pt: \(\sqrt{2x+4}+\sqrt[3]{3x+1}-3+\sqrt{\frac{2016}{2017}}=0\)
Chắc chắn rằng ngay cả người ra đề cũng không thể giải ra nghiệm chính xác của pt trên khi mà dạng của nó như dưới đây :)


a/ ĐK x>0
\(log_{2017}x+log_{2016}x=0\Leftrightarrow\dfrac{lnx}{ln2017}+\dfrac{lnx}{ln2016}=0\)
\(\Leftrightarrow lnx\left(\dfrac{1}{ln2017}+\dfrac{1}{ln2016}\right)=0\Leftrightarrow lnx=0\Rightarrow x=1\)
b/ ĐK \(\left\{{}\begin{matrix}x-1>0\\x-1\ne1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>1\\x\ne2\end{matrix}\right.\)
\(x^3-5x^2+6x=0\Leftrightarrow x\left(x^2-5x+6\right)=0\Rightarrow\left[{}\begin{matrix}x=0\left(l\right)\\x=2\left(l\right)\\x=3\end{matrix}\right.\) \(\Rightarrow x=3\)

\(y'=2016x^{2015}.\left(x^2+1\right)^{2017}+2017\left(x^2+1\right)^{2016}.2x.x^{2016}\)
\(y'=x^{2015}\left(x^2+1\right)^{2016}\left(2016\left(x^2+1\right)+2017.2x^2\right)\)
\(y'=x^{2015}\left(x^2+1\right)^{2016}\left(2016x^2+2016+2017.2x^2\right)\)
\(y'=0\Rightarrow x=0\)
Hàm số có 1 cực trị duy nhất

ý D có thể xảy ra vì gt chỉ cho h/s đồng biến trên (0;+\(\infty\))
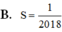
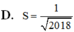




Đáp án C