Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
V = 1 2 ∫ − R R R 2 − x 2 . h R d x = 1 2 h R 2 R 3 − 2 R 3 3 = 2 R 2 h 3 = 2 R 3 tan φ 3
(Với h = M N ; tan φ = h R ) . Do đó V = 2.6 2 .10 3 = 240 c m 3

Đáp án D
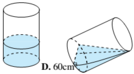
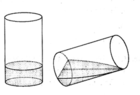
Dựng hệ trục tọa độ Oxy. Gọi S(x) là diện tích thiết diện do mặt phẳng có phương vuông góc với trục Ox với khối nước. Mặt phẳng này cắt trục Ox tại điểm có hoành độ h ≥ x ≥ 0 .
Gọi R, r lần lượt là bán kính đáy cốc thủy tinh và bán kính nửa đường tròn thiết diện.
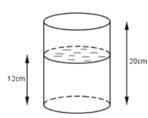
Gọi h là chiều cao của cốc nước. Do đó: R = 3cm, h = 10cm.
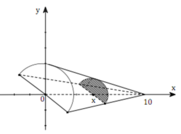
Vì thiết diện này là nửa đường tròn bán kính r nên



Cách giải:
Để uống được nước thì con quạ phải thả các viên bi vào cốc sao cho mực nước trong cốc dâng lên ít nhất: 20 -12 - 6 = 2( cm)
Khi đó, thể tích của mực nước dâng lên là


Đáp án D
Phương pháp:
+) Thể tích khối nước ít nhất cần dâng lên = Tổng thể tích đá thả vào.
+) Số viên đá = Tổng thể tích đá thả vào : Thể tích 1 viên đá


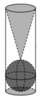
Gọi bán kính đáy của cốc hình trụ là R. Suy ra chiều cao của cốc nước hình trụ là 6R bán kính của viên bi là R; bán kính đáy hình nón là R; chiều cao của hình nón là 4R
Thể tích khối nón là ![]() Thể tích khối nón là
Thể tích khối nón là ![]()
Thể tích của cốc (thể tích lượng nước ban đầu) là ![]()
Suy ra thể tích nước còn lại: ![]() Vậy
Vậy 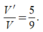
Chọn D.
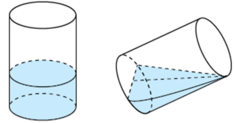
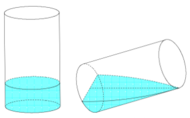





Đáp án D
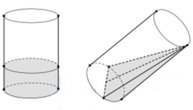
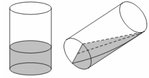
+) Chọn hệ trục tọa độ Oxy như hình vẽ. R = 4 c m là bán kính đáy cốc, h = 12 c m là chiều cao
của cốc.
+) Thiết diện cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x − 4 ≤ x ≤ 4 là một tam giác ABC vuông tại B có độ dài cạnh B C = R 2 − x 2 = 16 − x 2 và B A = R 2 − x 2 . h R = 16 − x 2 . 12 4 = 3 16 − x 2
+) Diện tích thiết diện là S x = 1 2 16 − x 2 .3 16 − x 2 = 3 2 16 − x 2 c m 2 .
+) Thể tích khối nước trong cốc là V = ∫ − 4 4 3 2 16 − x 2 d x = 3 2 16 x − x 3 3 4 − 4 = 128 c m 3
Chú ý: Có thể tính thể tích hình trên bằng công thức tính nhanh
+) Với R=4 cm, h=12 cm thể tích cần tìm V = 2 3 .4 2 .12 = 128 c m 3 .