Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Phương pháp:
+) Thể tích khối nước ít nhất cần dâng lên = Tổng thể tích đá thả vào.
+) Số viên đá = Tổng thể tích đá thả vào : Thể tích 1 viên đá
Đáp án B
Phương pháp:
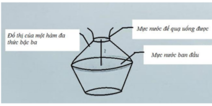
- Gắn hệ trục tọa độ Oxy, xác định phương trình hàm số bậc ba.
- Ứng dụng tích phân vào tính thể tích.
Cách giải:
Gắn hệ trục tọa độ Oxy như hình vẽ.
Gọi phương trình của đường sinh là: 
Theo đề bài, ta có: (C) có điểm cực đại (0;3), điểm cực tiểu là (2;1)
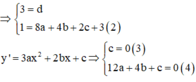
Từ (1),(2),(3) và (4)
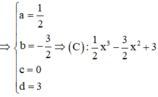
Thể tích đã cho vào:
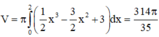
Thể tích 1 viên bi là
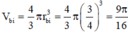
Cần số viên bi: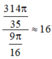 
(viên)
Thể tích khối nước trong cốc là
Thể tích của khối cầu là 4 3 πR 3
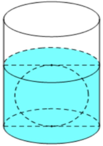
Sau khi thả viên bi, chiều cao của mực nước bằng đường kính khối cầu nên tổng thể tích của nước và khối cầu là
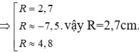
vậy R=2,7cm.
Chọn đáp án D.
Đáp án B
Phương pháp:
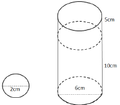
Tính thể tích mỗi viên bi hình cầu: V = 4 3 π R 3 ⇒ 5 viên có thể tích
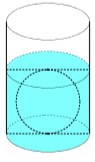
Tính thể tích lượng nước ban đầu (cột nước hình trụ): V 2 = V n = π R 2 h .
Tính tổng thể tích cả bi và nước lúc sau V = V 1 + V 2 , từ đó suy ra chiều cao cột nước lúc sau và khoảng cách từ mặt nước đến miệng cốc.
Cách giải:
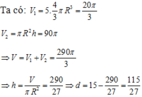
Chú ý khi giải:
Các em có thể sẽ quên không tính thể tích của 5 viên bi, hoặc nhầm lẫn đường kính 6cm thành bán kinh 6cm dẫn đến các thể tích bị sai.
Đáp án D
Tổng thể tích nước và 5 viên bi là: 120 + 5. 4 π .1 3 3 ≈ 140 , 94 m l
Lượng nước trong cốc có dạng hình trụ, với bán kính là: 6 − 0 , 2.2 2 = 2 , 8 c m
Khi đó, chiều cao h' của mực nước tinh từ đáy trong của cốc được tính từ:
π .2 , 8 2 h ' = 140 , 94 ⇔ h ' = 5 , 72
Chiều cao từ đáy trong côc đến mép cốc là: 9 − 1 = 8
Vậy mặt nước trong cách mép: 8 − 5.72 = 2 , 28.
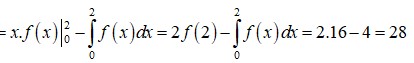
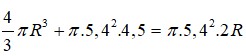
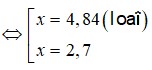
Cách giải:
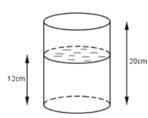
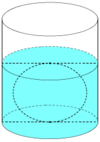
Để uống được nước thì con quạ phải thả các viên bi vào cốc sao cho mực nước trong cốc dâng lên ít nhất: 20 -12 - 6 = 2( cm)
Khi đó, thể tích của mực nước dâng lên là