Câu 4. Cho tam giác ABC, đường phân giác AD (D thuộc BC), kẻ tia Dx song song với AB, tia Dx cắt AC tại E. Chứng minh tam giác ADE là tam giác cân.Câu 5. Cho tam giác ABC có AB = 6cm, AC = 8cm và BC = 10cm.a) Chứng tỏ tam giác ABC vuông.b) Kẻ phân giác BD và CE (D thuộc AC, E thuộc AB), BD và CE cắt nhau tại I. Tính góc BICCâu 6. Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC (H thuộc vẽ tia Bx song song với AH). Trên Bx...
Đọc tiếp
Câu 4. Cho tam giác ABC, đường phân giác AD (D thuộc BC), kẻ tia Dx song song với AB, tia Dx cắt AC tại E. Chứng minh tam giác ADE là tam giác cân.
Câu 5. Cho tam giác ABC có AB = 6cm, AC = 8cm và BC = 10cm.
a) Chứng tỏ tam giác ABC vuông.
b) Kẻ phân giác BD và CE (D thuộc AC, E thuộc AB), BD và CE cắt nhau tại I. Tính góc BIC
Câu 6. Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC (H thuộc vẽ tia Bx song song với AH). Trên Bx lấy D sao cho BD = AH.
a) Chứng minh ΔAHB và ΔDHB bằng nhau.
b) Nếu AC = 12cm; BC =15cm. Tính độ dài DH.
Câu 7. Cho tam giác ABC vuông tại B có góc B1=B2 ; Â=60o, kẻ BH vuông góc với AC (H thuộc AC). Qua B kẻ đường thẳng d song song với AC.
a) Tính góc ABH.
b) Chứng minh đường thẳng d vuông góc với BH.
Câu 8. Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M. Trên tia đối của tia CB lấy điểm N sao cho BM = CN.
a) Chứng minh ΔAMN là tam giác cân.
b) Kẻ BH vuông góc với AM (H thuộc AM), CK vuông góc với AN (K thuộc AN). Chứng minh rằng BH = CK.
c) Gọi O là giao điểm của BH và CK. Chứng minh ΔOBC cân.
d) Gọi D là trung điểm của BC. Chứng minh rằng A, D, O thẳng hàng.
Câu 9. Cho tam giác ABC, điểm D thuộc cạnh BC. Gọi M là trung điểm của AD. Trên tia đối của tia MB lấy điểm E sao cho ME = MB. Trên tia đối của tia MC lấy F sao cho MF = MC. Chứng minh:
a) AE = BD;
b) AF // BC.
c) Ba điểm A, E, F thẳng hàng.
Câu 10. Cho tam giác ABC cân tại A, M là trung điểm của BC.
a) Chứng minh góc AFE = gócABC⇒EF//BC và ΔABM=ΔACM.
b) Chứng minh AM⊥BC.
c) Trên cạnh BA lấy điểm E. Trên cạnh CA lấy điểm F sao cho BE = CF. Chứng minh ΔEBC và ΔFCB bằng nhau.
d) Chứng minh EF // BC.


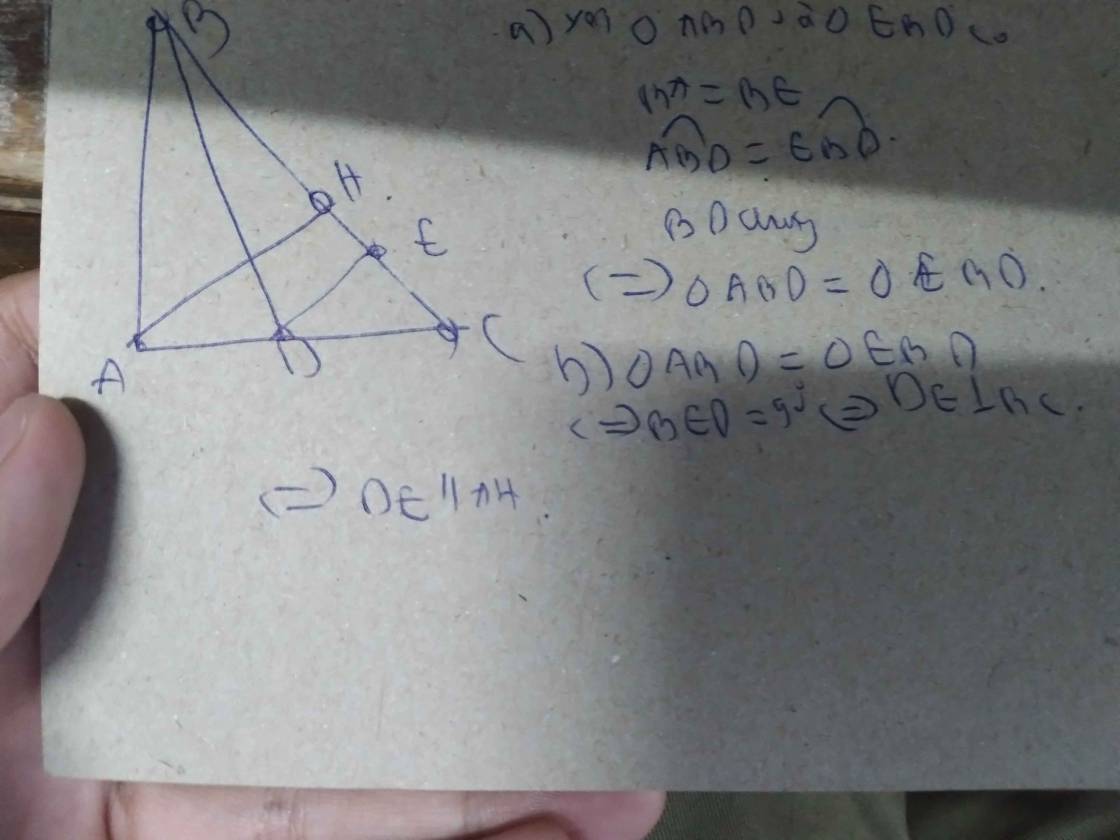
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC, ta được:
\(AB^2=AH\cdot AC\)
\(\Leftrightarrow AB\cdot AB=AH\cdot AC\)
\(\Leftrightarrow\dfrac{AH}{AB}=\dfrac{AB}{AC}\)(1)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{AB}{AC}=\dfrac{BD}{DC}\)(Tính chất đường phân giác của tam giác)(2)
Từ (1) và (2) suy ra \(\dfrac{AH}{AB}=\dfrac{BD}{DC}\)(3)
Ta có: BH⊥AC(gt)
DE⊥AC(gt)
Do đó: BH//DE(Định lí 1 từ vuông góc tới song song)
Xét ΔBHC có BH//DE(cmt)
nên \(\dfrac{BD}{DC}=\dfrac{EH}{EC}\)(Định lí Ta lét)(4)
Xét ΔAHB có AF là đường phân giác ứng với cạnh BH(gt)
nên \(\dfrac{AH}{AB}=\dfrac{HF}{FB}\)(Định lí đường phân giác của tam giác)(5)
Từ (3), (4) và (5) suy ra \(\dfrac{HF}{FB}=\dfrac{HE}{EC}\)
Xét ΔHBC có
F∈HB(gt)
E∈HC(gt)
\(\dfrac{HF}{FB}=\dfrac{HE}{EC}\)(cmt)
Do đó: EF//BC(Định lí Ta lét đảo)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC, ta được:
AB2=AH⋅ACAB2=AH⋅AC
⇔AB⋅AB=AH⋅AC⇔AB⋅AB=AH⋅AC
⇔AHAB=ABAC⇔AHAB=ABAC(1)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên ABAC=BDDCABAC=BDDC(Tính chất đường phân giác của tam giác)(2)