Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

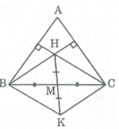
Ta có K là điểm đối xứng của H qua tâm M nên MK = MH
Xét tứ giác BHCK, ta có:
BM = MC (gt)
MK = MH (chứng minh trên)
Suy ra: Tứ giác BHCK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Suy ra: KB // CH, KC // BH
Ta có: CH ⊥ AB (gt)
Suy ra: KB ⊥ AB nên ∠ (KBA) = 90 0
Ta có: BH ⊥ AC (gt)
Suy ra: CK ⊥ AC nên ∠ (KCA) = 90 0

Ta có K là điểm đối xứng của H qua tâm M nên MK = MH
Xét tứ giác BHCK ta có:
BM = MC (gt)
MK = MH (chứng minh trên)
Suy ra: Tứ giác BHCK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Suy ra: KB // CH, KC // BH
CH ⊥ AB (gt)
\(\Rightarrow KB\perp AB\Rightarrow\widehat{KBA}=90^0\)
BH ⊥ AC (gt)
\(\Rightarrow CK\perp AC\Rightarrow\widehat{KCA}=90^0\)

a) Có M là td BC
MH = MK ( K đối xứng H qua M)
Suy ra M là td mỗi đg
suy ra BHCK là hbh
Vậy...
b) có ch là đường cao tam giác ABC ( H là trực tâm)
suy ra CH vuông góc AB
có bhck là hình bình hành
=> DK song song với CH
Suy ra DK vuông góc AB
Vậy góc ABK bằng 90 độ
C) BHCK là hình thoi
Khi và chỉ khi BH = CH
Khi và chỉ khi H là trọng tâm của tam giác ABC
Khi và chỉ khi tam giác ABC đều
Vận tam giác ABC đều thì tứ giác BHCK là hình thoi
Biết bạn đề bài này lâu rồi nhưng mà mình cứ giải Xem cách của mình với các của bạn cách nào tiện hơn hihi

Xet tứ giác BHCK có
MH=MK; MB=MC => BHCK là hình bình hành (Tứ giác có các cặp cạnh đối cắt nhau tại trung điểm mỗi đường là hbh)
=> CK//BH mà BH vuông góc với AC => CK vuông góc với AC => \(\widehat{ACK}=90^o\)
=> BK//CH mà CH vuông góc với AB => BK vuông góc với AB => \(\widehat{ABK}=90^o\)