Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác ABM và tam giác ACN:
Góc A chung
AB = AC (do tam giác ABC cân tại A)
AM = AN (gt)
Suy ra: tam giác ABM = tam giác ACN (c g c)
b) Xét tam giác AMN có :
AM =AN (gt)
Suy ra: tam giác AMN cân tại A
Suy ra góc ANM = \(\dfrac{\text{180 - góc A}}{2}\)
mà góc ABC = \(\dfrac{\text{180 - góc A}}{2}\) ( do tam giác ABC cân tại A)
Suy ra: góc ANM = góc ABC
Mà 2 góc này ở vị trí đồng vị của MN và BC
Suy ra MN song song BC

a: AM+MC=AC
NA+NB=AB
mà AB=AC; AM=AN
nên MC=NB
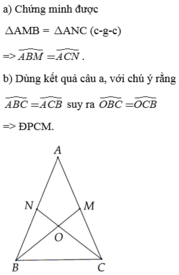
b: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
BC chung
=>ΔNBC=ΔMCB
=>góc OBC=góc OCB
=>ΔOBC cân tại O

xét TG AMC và TG ANB có
AC=AB (TG ABC cân tại A)
G A chung
AM=AN (GT)
S ra TG AMC=TG ANB (c.g.c)
S ra CM=BN (2 cạnh tg ứng)
b) Vì TG AMC=TG ANB (cmt)
S ra G ACM=G ABN (2 góc tg ứng)
* G ACM+G MCB = G ACB
G ABN+G NBC = G ABC
mà G ACM=G ABN (cmt)
G ACB=G ABC ( TG ABC cân tại A)
S raG MCB=G NBC
S ra TG OBC cân tại O
(2 góc ở đấy bằng nhau)
xét TG AMC và TG ANB có
AC=AB (TG ABC cân tại A)
G A chung
AM=AN (GT)
S ra TG AMC=TG ANB (c.g.c)
S ra CM=BN (2 cạnh tg ứng)
b) Vì TG AMC=TG ANB (cmt)
S ra G ACM=G ABN (2 góc tg ứng)
* G ACM+G MCB = G ACB
G ABN+G NBC = G ABC
mà G ACM=G ABN (cmt)
G ACB=G ABC ( TG ABC cân tại A)
S raG MCB=G NBC
S ra TG OBC cân tại O
(2 góc ở đấy bằng nhau)

a) Xét ΔABN và ΔACM có
AB=AC(ΔABC cân tại A)
\(\widehat{BAN}\) chung
AN=AM(gt)
Do đó: ΔABN=ΔACM(c-g-c)
Suy ra: BN=CM(hai cạnh tương ứng)
b) Xét ΔAHB và ΔAHC có
AB=AC(ΔABC cân tại A)
AH chung
HB=HC(H là trung điểm của BC)
Do đó: ΔAHB=ΔAHC(c-c-c)
Suy ra: \(\widehat{AHB}=\widehat{AHC}\)(hai góc tương ứng)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
hay AH⊥BC(đpcm)
c) Ta có: AH⊥BC(cmt)
mà H là trung điểm của BC(gt)
nên AH là đường trung trực của BC
⇔EH là đường trung trực của BC
⇔EB=EC(Tính chất đường trung trực của một đoạn thẳng)
Xét ΔEBC có EB=EC(cmt)
nên ΔEBC cân tại E(Định nghĩa tam giác cân)