Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
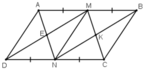
ABCD là hình bình hành ⇒ AB = CD.
M là trung điểm AB ⇒ AM = MB = AB/2.
N là trung điểm CD ⇒ CN = DN = CD/2.
⇒ AM = MB = CN = DN.
+ Tứ giác BMDN có: BM // DN và BM = DN
⇒ BMDN là hình bình hành
⇒ DM // BN hay ME // NK
+ Tứ giác AMCN có: AM // NC, AM = NC
⇒ AMCN là hình bình hành
⇒ AN // CM hay EN // MK.
+ Tứ giác MENK có: ME // NK và NE // MK
⇒ MENK là hình bình hành.
a) MENK là hình thoi
⇔ MN ⊥ EK.
⇔ CD ⊥ AD (Vì EK // CD và MN // AD)
⇔ ABCD là hình chữ nhật.
b) MENK là hình chữ nhật
⇔ MN = EK
Mà MN = BC;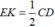 
(vì tam giác MCD có E và K lần lượt là trung điểm MD, MC nên EK là đường trung bình của tam giác MCD).
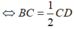
⇔ CD = 2.BC.
c) MENK là hình vuông
⇔ MENK là hình thoi và đồng thời là hình chữ nhật
⇔ ABCD là hình chữ nhật và có CD = 2.BC.
1: Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
Suy ra: Hai đường chéo AN cắt MD tại trung điểm của mỗi đường
=>K là trung điểm chung của AN và MD
Xét tứ giác MBCN có
MB//CN
MB=CN
Do đó: MBCN là hình bình hành
Suy ra: Hai đường chéo MC và BN cắt nhau tại trung điểm của mỗi đường
=>L là trung điểm chung của BN và CM
2: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
Suy ra: Hai đường chéo AC và MN cắt nhau tại trung điểm của mỗi đường(1)
Xét tứ giác MKNL có
MK//NL
ML//NK
Do đó: MKNL là hình bình hành
Suy ra: Hai đường chéo MN và KL cắt nhau tại trung điểm của mỗi đường(2)
Ta có: ABCD là hình bình hành
nên Hai đườg chéo AC và BD cắt nhau tại trung điểm của mỗi đường(3)
Từ (1), (2) và (3) suy ra AC,BD,MN,KL đồng quy