Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
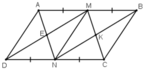
ABCD là hình bình hành ⇒ AB = CD.
M là trung điểm AB ⇒ AM = MB = AB/2.
N là trung điểm CD ⇒ CN = DN = CD/2.
⇒ AM = MB = CN = DN.
+ Tứ giác BMDN có: BM // DN và BM = DN
⇒ BMDN là hình bình hành
⇒ DM // BN hay ME // NK
+ Tứ giác AMCN có: AM // NC, AM = NC
⇒ AMCN là hình bình hành
⇒ AN // CM hay EN // MK.
+ Tứ giác MENK có: ME // NK và NE // MK
⇒ MENK là hình bình hành.
a) MENK là hình thoi
⇔ MN ⊥ EK.
⇔ CD ⊥ AD (Vì EK // CD và MN // AD)
⇔ ABCD là hình chữ nhật.
b) MENK là hình chữ nhật
⇔ MN = EK
Mà MN = BC;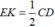 
(vì tam giác MCD có E và K lần lượt là trung điểm MD, MC nên EK là đường trung bình của tam giác MCD).
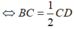
⇔ CD = 2.BC.
c) MENK là hình vuông
⇔ MENK là hình thoi và đồng thời là hình chữ nhật
⇔ ABCD là hình chữ nhật và có CD = 2.BC.
Câu 1:
a)
\(BM=MC=\frac{1}{2}BC\) (M là trung điểm của BC)
\(AN=ND=\frac{1}{2}AD\) (N là trung điểm của AD)
mà \(BC=AD\) (ABCD là hình bình hành)
\(\Rightarrow AN=ND=BM=MC\) (1)
mà ND // BM
=> BMDN là hình bình hành
=> BN // MD (2)
=> MDKB là hình thang
b)
MC = AN (theo 1)
mà MC // AN (ABCD là hình bình hành)
=> AMCN là hình bình hành
=> AM // CN (3)
Từ (2) và (3)
=> MPNQ là hình bình hành (4)
BM = AN (theo 1)
mà BM // AN (ABCD là hình bình hành)
=> ABMN là hình bình hành
mà AB = BM \(\left(=\frac{1}{2}BC\right)\)
=> ABMN là hình thoi
=> AM _I_ BN
=> MPN = 900 (5)
Từ (4) và (5)
=> MPNQ là hình chữ nhật
c)
MPNQ là hình vuông
<=> MN là tia phân giác của PMQ
mà MN là đường trung tuyến của tam giác MDA vuông tại M (N là trung điểm của AD; MPNQ là hình chữ nhật)
=> Tam giác MDA vuông cân tại M có MN là đường trung tuyến
=> MN là đường cao của tam giác MDA
=> MNA = 900
mà MNA = ABM (ABMN là hình thoi)
=> ABM = 900
mà ABCD là hình bình hành
=> ABCD là hình chữ nhật
Câu 2:
a)
\(AE=EB=\frac{AB}{2}\) (E là trung điểm của của AB)
\(CF=FD=\frac{CD}{2}\) (F là trung điểm của của CD)
mà AB = CD (ABCD là hình bình hành)
=> AE = EB = CF = FD (1)
mà AE // CF (ABCD là hình bình hành)
=> AECF là hình bình hành
b)
AE = FD (theo 1)
mà AE // FD (ABCD là hình bình hành)
=> AEFD là hình bình hành
mà DA = AE \(\left(=\frac{1}{2}AB\right)\)
=> AEFD là hình thoi
=> AF _I_ ED
=> EMF = 900 (2)
EB = FD (theo 1)
mà EB // FD (ABCD là hình bình hành)
=> EBFD là hình bình hành
=> EM // NF
mà EN // MF (AECF là hình bình hành)
=> EMFN là hình bình hành
mà EMF = 900 (theo 2)
=> EMFN là hình chữ nhật
c)
EMFN là hình vuông
<=> EF là tia phân giác của MEN
mà EF là đường trung tuyến của tam giác ECD vuông tại E (F là trung điểm của CD; EMFN là hình chữ nhật)
=> Tam giác ECD vuông cân tại E có EF là đường trung tuyến
=> EF là đường cao của tam giác ECD
=> EFD = 900
mà EFD = DAE (AEFD là hình thoi)
=> DAE = 900
mà ABCD là hình bình hành
=> ABCD là hình chữ nhật
1:
Xet ΔOAE và ΔOCF có
góc OAE=góc OCF
góc AOE=góc COF
=>ΔOAE đồng dạng với ΔOCF
=>AE/CF=OE/OF
Xét ΔOEB và ΔOFD có
góc OEB=góc OFD
góc EOB=góc FOD
=>ΔOEB đồng dạng với ΔOFD
=>EB/FD=OE/OF=AE/CF
mà CF=DF
nên EB=AE
=>E là trung điểm của BA
1: Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
Suy ra: Hai đường chéo AN cắt MD tại trung điểm của mỗi đường
=>K là trung điểm chung của AN và MD
Xét tứ giác MBCN có
MB//CN
MB=CN
Do đó: MBCN là hình bình hành
Suy ra: Hai đường chéo MC và BN cắt nhau tại trung điểm của mỗi đường
=>L là trung điểm chung của BN và CM
2: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
Suy ra: Hai đường chéo AC và MN cắt nhau tại trung điểm của mỗi đường(1)
Xét tứ giác MKNL có
MK//NL
ML//NK
Do đó: MKNL là hình bình hành
Suy ra: Hai đường chéo MN và KL cắt nhau tại trung điểm của mỗi đường(2)
Ta có: ABCD là hình bình hành
nên Hai đườg chéo AC và BD cắt nhau tại trung điểm của mỗi đường(3)
Từ (1), (2) và (3) suy ra AC,BD,MN,KL đồng quy
