Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

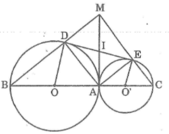
Tứ giác ADME là hình chữ nhật và ID = IE (chứng minh trên) nên đường chéo AM của hình chữ nhật phải đi qua trung điểm I của DE. Suy ra: A, I, M thẳng hàng.
Ta có: IA ⊥ OO’ (vì IA là tiếp tuyến của (O))
Suy ra: AM ⊥ OO’
Vậy MA là tiếp tuyến chung của đường tròn (O) và (O’)

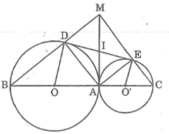
Kẻ tiếp tuyến chung tại A cắt DE tại I
Trong đường tròn (O) ta có:
IA = ID (tính chất hai tiếp tuyến cắt nhau)
Trong đường tròn (O’) ta có :
IA = IE (tính chất hai tiếp tuyến cắt nhau)
Suy ra : IA = ID = IE = (1/2).DE
Tam giác ADE có đường trung tuyến AI ứng với cạnh DE và bằng nửa cạnh DE nên tam giác ADE vuông tại A
Suy ra: 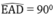

a: Kẻ tiếp tuyến chung AH của (O) và (O'). (H thuộc DE)
Xét (O) có
HA,HD là tiếp tuyến
nên HO là phân giác của góc DHA(1) và HD=HA
mà OD=OA
nên OH là trung trực của AD
=>OH vuông góc với AD tại K
Xét (O') có
HA,HE là tiếp tuyến
nên HA=HE và HO' là phân giác của góc AHE(2)
mà O'A=O'E
nên O'H là trung trực của AE
=>O'H vuông góc với AE tại G
Từ (1), (2) suy ra góc OHO'=1/2*180=90 độ
Xét tứ giác HKAG có
góc KHG=góc HKA=góc HGA=90 độ
nên HKAG là hình chữ nhật
=>góc DAE=90 độ
b: Xét (O) có
ΔBAD nội tiếp
BA là đường kính
=>ΔBAD vuông tại D
=>góc MDA=90 độ
Xét (O') có
ΔAEC nội tiếp
AC là đường kính
=>ΔAEC vuông tại E
=>góc MEA=90 độ
Xét tứ giác MDAE có
góc MDA=góc MEA=góc DAE=90 độ
nên MDAE là hình chữ nhật

Giải:
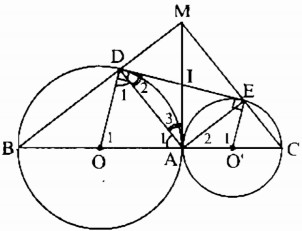
a) Kẻ tiếp tuyến chung tại A cắt DE tại I
Trong đường tròn (O) ta có:
IA = ID (tính chất hai tiếp tuyến cắt nhau)
Trong đường tròn (O’) ta có:
Quảng cáo
IA = IE (tính chất hai tiếp tuyến cắt nhau)
Suy ra: IA=ID=IE=12DEIA=ID=IE=12DE
Tam giác ADE có đường trung tuyến AI ứng với cạnh DE và bằng nửa cạnh DE nên tam giác ADE vuông tại A.
Suy ra: ˆEAD=90∘EAD^=90∘
b) Tam giác ABD nội tiếp trong đường tròn (O) có AB là đường kính nên ˆADB=90∘ADB^=90∘ hay ˆAEM=90∘AEM^=90∘
Mặt khác: ˆEAD=90∘EAD^=90∘ (chứng minh trên)
Tứ giác ADME có ba góc vuông nên nó là hình chữ nhật.
c) Tứ giác ADME là hình chữ nhật và ID = IE (chứng minh trên) nên đường chéo
AM của hình chữ nhật phải đi qua trung điểm I của DE. Suy ra: A, I, M thẳng hàng.
Ta có: IA ⊥ OO’ ( vì IA là tiếp tuyến của (O))
Suy ra: AM ⊥ OO’
Vậy MA là tiếp tuyến chung của đường tròn (O) và (O’).

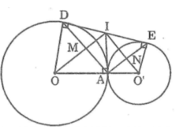
Trong đường tròn (O) ta có OI là tia phân giác của góc AID (tính chất hai tiếp tuyến cắt nhau)
Trong đường tròn (O’) ta có O’I là tia phân giác của góc AIE (tính chất hai tiếp tuyến cắt nhau)
=> IO ⊥ IO’ (tính chất hai góc kề bù)
Suy ra 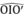 =
90
°
hay
=
90
°
hay  =
90
°
=
90
°
Lại có: IA = ID (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác ADI cân tại I
Tam giác cân AID có IO là phân giác của góc AID nên IO cũng là đường cao của tam giác AID
Suy ra: IO ⊥ AD hay 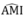 =
90
°
=
90
°
Mặt khác: IA = IE (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác AEI cân tại I
Tam giác cân AIE có IO’ là phân giác của góc AIE nên IO’ cũng là đường cao của tam giác AIE
Suy ra: IO’ ⊥ AE hay  =
90
°
=
90
°
Tứ giác AMIN có ba góc vuông nên nó là hình chữ nhật.


Tam giác ABD nội tiếp trong đường tròn (O) có AB là đường kính nên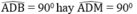
Tam giác AEC nội tiếp trong đường tròn (O’) có AC là đường kính nên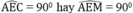
Mặt khác: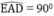 (chứng minh trên)
(chứng minh trên)
Tứ giác ADME có ba góc vuông nên nó là hình chữ nhật.