Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi tắt là bất đẳng thức Cauchy, sử dụng để chứng minh bất đẳng thức số có điều kiện lớn hơn 0
Đây là công thức tổng quát:
bạn đặt câu hỏi quá chung mình không biết là bạn muốn hỏi cách chứng minh hay là gì để trả lời rõ:p

\(\frac{a+b}{2}\ge\sqrt{ab}\Leftrightarrow a+b\ge2\sqrt{ab}\)
<=>\(a+b-2\sqrt{ab}\ge0\)
<=>\(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\)(luôn đúng)
=>dpcm

<=> \(a+b\ge2\sqrt{ab}\)
<=> \(a+b-2\sqrt{ab}\ge0\)
<=. \(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\)(luôn đúng )
dấu = khi a=b

bất đẳng thức cosi là khái niệm dùng để chỉ bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm. Trong đó, trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng
Hệ quả 1: Nếu tổng hai số dương không đổi thì tích của chúng lớn nhất khi hai số đó bằng nhau Hệ quả 2: Nếu tích hai số dương không đổi thì tổng của hai số này nhỏ nhất khi hai số đó bằng nhau

\(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\Leftrightarrow a+b-2\sqrt{ab}\ge0\Leftrightarrow a+b\ge2\sqrt{ab}\Leftrightarrow\frac{a+b}{2}\ge\sqrt{ab}\)

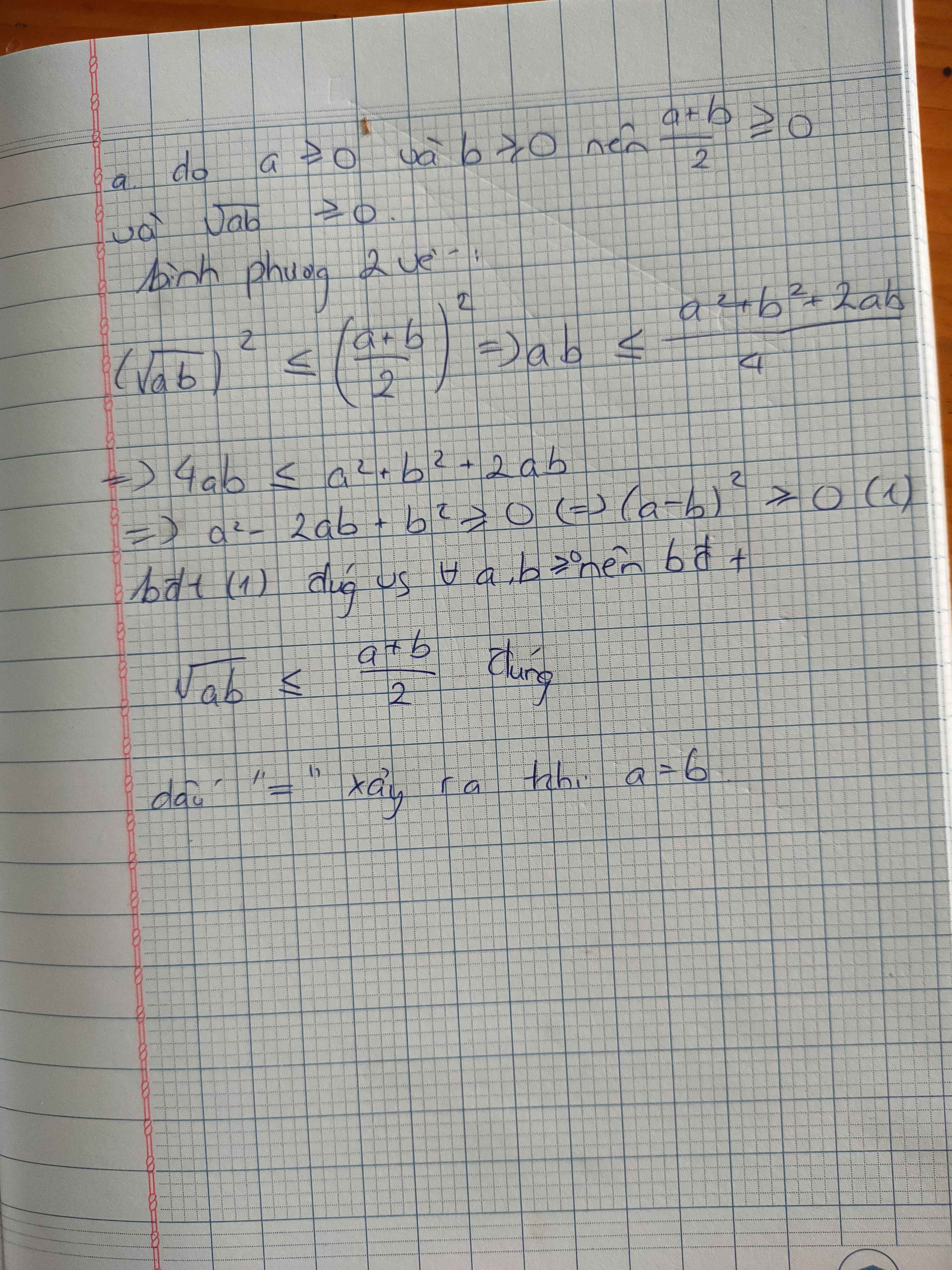
Hai bđt đó là một đấy bạn.
Ngoài ra còn có tên là BĐT Cauchy dạng Engel nữa mà mình ko biết Engel là gì cả?:)
Chữ Svac-xơ được phiên âm từ chữ Schwarz ra mà bạn
Engel là lấy theo tên nhà toán học Đức Arthur Engel thì phải