LP
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LP
0
19 tháng 12 2021
a: \(\Leftrightarrow a^2-4a+4+b^2-6b+9+c^2-2c+1>=0\)
\(\Leftrightarrow\left(a-2\right)^2+\left(b-3\right)^2+\left(c-1\right)^2>=0\)
Dấu '=' xảy ra (a,b,c)=(2;3;1)
AH
Akai Haruma
Giáo viên
3 tháng 3 2021
Lời giải:
Ta có:
$a^3+b^3-ab(a+b)=(a-b)^2(a+b)\geq 0$ với mọi $a\geq 0; b\geq 0$
$\Rightarrow a^3+b^3\geq ab(a+b)$
Dấu "=" xảy ra khi $a=b$
DN
1 tháng 8 2017
1. Ta có: \(a-b+\dfrac{4}{\left(a-b\right)\left(b+1\right)^2}\ge\dfrac{4}{b+1}\)
\(a+\dfrac{4}{\left(a-b\right)\left(b+1\right)^2}\ge\dfrac{4}{b+1}+b\)(1)
lại có: \(\dfrac{4}{b+1}+b+1\ge4\)
\(\dfrac{4}{b+1}+b\ge3\)(2)
Từ (1),(2) ta có:\(a+\dfrac{4}{\left(a-b\right)\left(b+1\right)^2}\ge3\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}a-b=\dfrac{4}{\left(a-b\right)\left(b+1\right)^2}\\b+1=\dfrac{4}{b+1}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\)
2. Ta có\(\dfrac{2a^3+1}{4b\left(a-b\right)}\ge3\)
\(\Leftrightarrow2a^3+1\ge12ab-12b^2\)
\(\Leftrightarrow2a^3+1-12ab+12b^2\ge0\)
\(\Leftrightarrow2a^3-3a^2+1+3\left(a-2b\right)^2\ge0\)
\(\Leftrightarrow\left(2a+1\right)\left(a-1\right)^2+3\left(a-2b\right)^2\ge0\)(luôn đúng)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}a-1=0\\a-2b=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=1\\b=\dfrac{1}{2}\end{matrix}\right.\)
PT
1
CM
13 tháng 4 2017
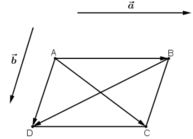
Có hai vec tơ a→, b→ bất kì như hình vẽ.
Vẽ hình bình hành ABCD sao cho 
Ta có:
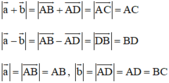
Do đó
a)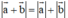 
⇔ AC = AB + BC ⇔ B nằm giữa A và C
⇔ 
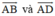cùng hướng hay a→ và b→ cùng hướng.
b)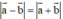 
⇔ AC = BD
⇔ ABCD là hình chữ nhật
⇔ AB ⊥ CD hay 
