Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(a+b+c=3\Rightarrow\left(a+b+c\right)^2=9\)
\(\Rightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=9\)
\(\Rightarrow a^2+b^2+c^2=9-2\left(ab+bc+ca\right)=9-2\times6=3\)
\(\Rightarrow a^2+b^2+c^2=ab+bc+ca\)
\(\Rightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca=0\)
\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Rightarrow a=b=c\)
Mà \(a+b+c=3\Rightarrow a=b=c=1\)
\(\Rightarrow A=\left(1-1\right)^{2019}+\left(1^2-1\right)^{2020}+\left(1^3-1\right)^{2021}\)
\(=0^{2019}+0^{2020}+0^{2021}=0\)

Em tham khảo cách làm tại link: Câu hỏi của Cao Chi Hieu - Toán lớp 9 - Học toán với OnlineMath

Ta có: \(2020+c^2=ab+bc+ca+c^2=\left(b+c\right)\left(c+a\right)\)
Tương tự => \(2020+a^2=\left(a+b\right)\left(c+a\right)\)
và \(2020+b^2=\left(a+b\right)\left(b+c\right)\)
=> PT = \(\frac{a-b}{\left(b+c\right)\left(c+a\right)}+\frac{b-c}{\left(a+b\right)\left(c+a\right)}+\frac{c-a}{\left(a+b\right)\left(b+c\right)}\)
= \(\frac{\left(a-b\right)\left(a+b\right)+\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(c+a\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\) = \(\frac{a^2-b^2+b^2-c^2+c^2-a^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\) = 0

\(\left(a-1\right)\left(b-1\right)\left(c-1\right)=\left(a-1\right)\left(bc-b-c+1\right)\)
\(=abc-\left(ab+bc+ca\right)+a+b+c-1\)
\(=abc-abc+1-1=0\) (đpcm)

Đặt \(\hept{\begin{cases}a+b=x\\a+c=y\\b+c=z\end{cases}}\)
Do a+b+c = 1 \(\Leftrightarrow x+y+z=2\)
Ta có :
\(\text{Sima}\frac{a+bc}{b+c}=\text{Sima}\frac{a\left(a+b+c\right)+bc}{b+c}=\text{Sima}\frac{a^2+ab+ac+bc}{b+c}=\text{Sima}\frac{\left(a+b\right)\left(a+c\right)}{b+c}\)
\(=\text{Sima}\frac{xy}{z}=\frac{xy}{z}+\frac{xz}{y}+\frac{yz}{x}\)
Ta có : \(2\text{Sima}\frac{xy}{z}=\left(\frac{xy}{z}+\frac{xz}{y}\right)+\left(\frac{xy}{z}+\frac{yz}{x}\right)+\left(\frac{xz}{y}+\frac{yz}{x}\right)\)
\(\ge2x+2y+2z\)
\(\Rightarrow\text{Sima}\frac{xy}{z}\ge x+y+z=2\) hay \(\text{Sima}\frac{a+bc}{b+c}\ge2\)(đpcm)

Bài 1:
\(HPT\Leftrightarrow\left(a+b+c\right)^2=0\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=0\\ \Leftrightarrow a^2+b^2+c^2=0\\ \Leftrightarrow a=b=c=0\left(a^2+b^2+c^2\ge0\right)\\ \Leftrightarrow A=\left(-1\right)^{2019}+\left(-1\right)^{2020}+\left(-1\right)^{2021}=-1+1-1=-1\)
Bài 2: Giải toán trên mạng - Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học trực tuyến OLM
Bài 3: Xác định a, b, c để x^3 - ax^2 + bx - c = (x - a) (x-b)(x-c) - Lê Tường Vy

Ta có
\(a+b+c=6\)
\(\Leftrightarrow\left(a+b+c\right)^2=36\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ca=36\)
Mà \(a^2+b^2+c^2=ab+bc+ca\)
Khi đó ta có
\(3\left(ab+bc+ca\right)=36\)
\(\Leftrightarrow ab+bc+ca=12\)
\(\Leftrightarrow\hept{\begin{cases}2ab+2bc+2ca=24\\2a^2+2b^2+2c^2=24\end{cases}}\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca=0\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}a-b=0\\b-c=0\\c-a=0\end{cases}\Leftrightarrow\hept{\begin{cases}a=b\\b=c\\c=a\end{cases}}}\Leftrightarrow a=b=c=\frac{6}{3}=2\) ( 1 )
Thay (1) vào C ta có
\(C=\left(1-2\right)^{2021}+\left(2-1\right)^{2021}+\left(2-2\right)^{2021}\)
\(=-1+1+0=0\)
Vậy ......................
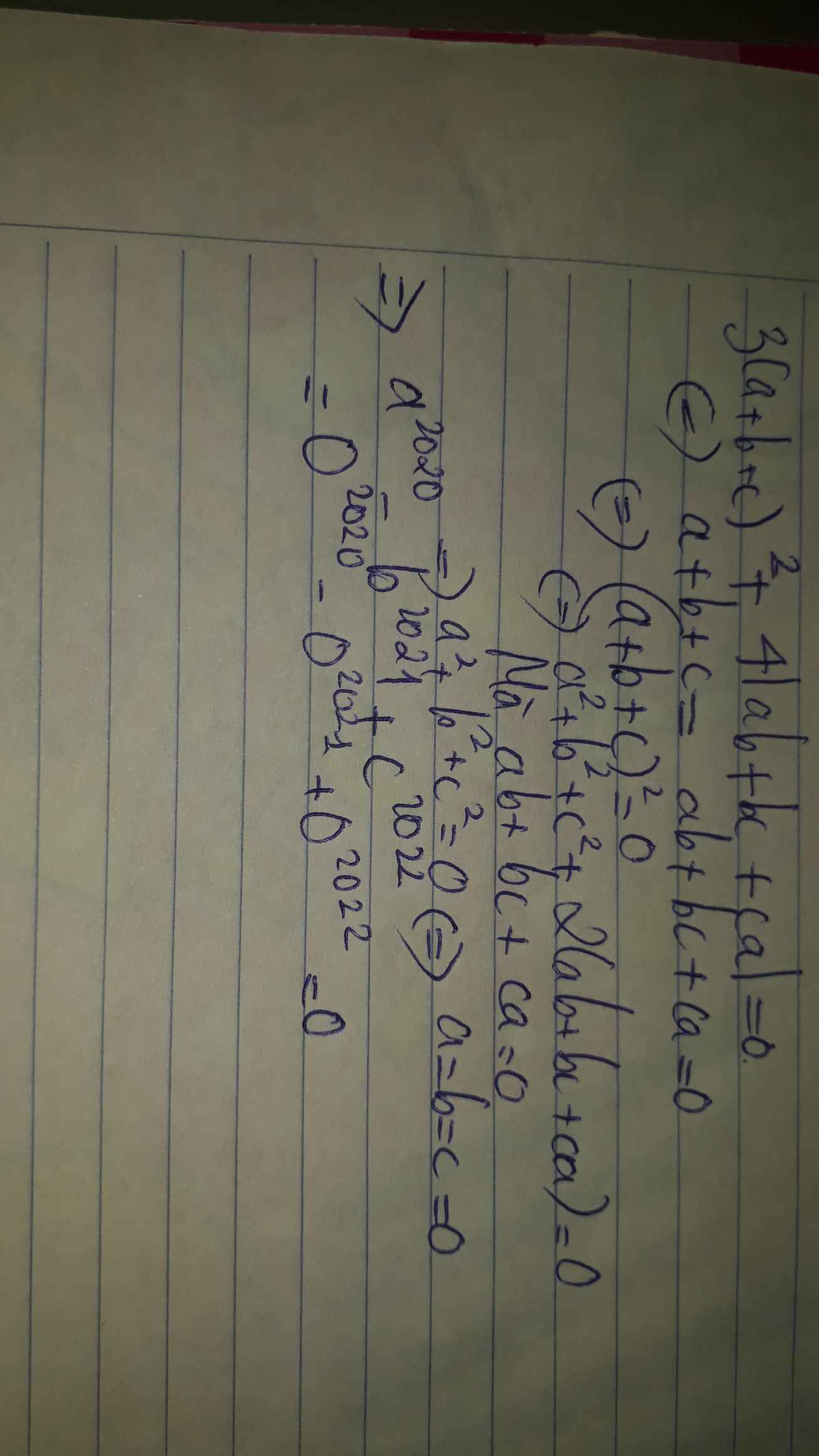
\(a^2+b^2+c^2-ab-bc-ac=0\)
\(\Rightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac=0\)
\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\) (1)
Mà: \(\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2\ge0\)
Nên PT (1) \(\Leftrightarrow\left\{{}\begin{matrix}\left(a-b\right)^2=0\\\left(b-c\right)^2=0\\\left(a-c\right)^2=0\end{matrix}\right.\)
=> a = b = c
\(P=\left(a-b\right)^{2020}+\left(b-c\right)^{2021}+\left(c-a\right)^{2022}\)
\(=\left(a-a\right)^{2020}+\left(b-b\right)^{2021}+\left(c-c\right)^{2022}\)
= 0